矩阵乘法加速递推式计算
前提
矩阵乘法板子
struct martix{
ll m[10][10];
void init(){clean(m,0);}
};
inline martix mutiply(martix input1,martix input2,int a,int b,int c){
martix output;
output.init();
loop(i,1,a){
loop(j,1,b){
loop(k,1,c){
output.m[i][k]+=input1.m[i][j]*input2.m[j][k];
output.m[i][k]%=mod;
}
}
}
return output;
}快速幂板子
inline martix fastpower(martix a,int times){
martix stag=a;
martix res=start_;//start_是单位矩阵,可以通过构造构造出此矩阵为对角线为1,其他都为0的矩阵
while(times){
if(times&1)res=mutiply(res,stag,2,2,2);
times>>=1;
stag=mutiply(stag,stag,2,2,2);
}
return res;
}fibonacci 第n项
转化过程
- StepOne:写出递推式:$f[i]=f[i-1]+f[i-2]$
- StepTwo:考虑矩阵
首先,$f[i]$是由$f[i-1],f[i-2]$得出来的,所以当前矩阵应该需要$f[i],f[i-1],f[i-2]$
然后根据所有的已知条件写出如下草稿:
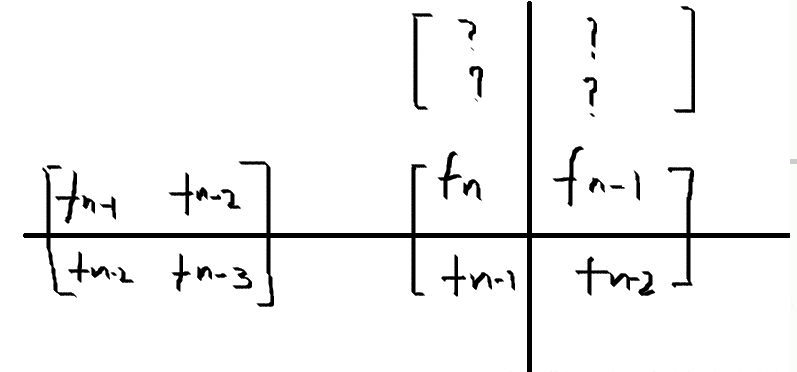
问号那一团就是我们要构造的转移矩阵
根据等量关系:
$$
f[n]=f[n-1]+f[n-2]\
$$
左边那一竖列问号应该是1
根据等量关系:
$$
f[n-1]=f[n-1]+0\times f[n-2]\
f[n-2]=f[n-2]+0\times f[n-1]
$$
右面一竖列问号号应该是1和0
最后构造出来的矩阵是:
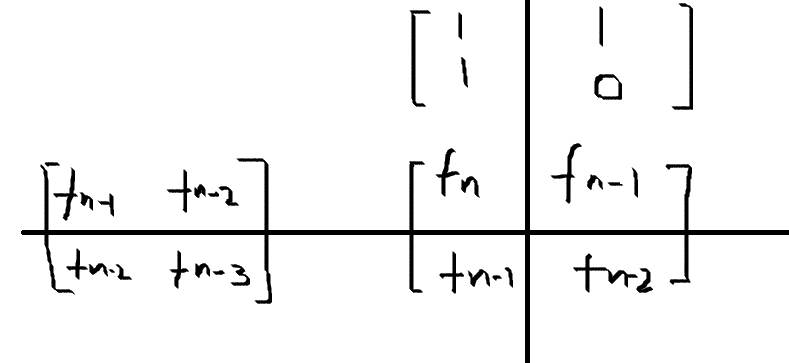
设构造出的转移矩阵为s,初始答案矩阵为a,,斐波那契数列的第n项为x,则
$$
a=\begin{pmatrix}
f[3] & f[2]\
f[2] &f[1]\
\end{pmatrix}
\s=
\begin{pmatrix}
1&1\1&0
\end{pmatrix}
\令矩阵k=a\times s^{n-3}
\x=k_{1\ 1}
$$
- StepThree:可以搞了:
#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define anti_loop(i,start,end) for(register int i=start;i>=end;--i)
#define ll long long
template<typename T>void read(T &x){
x=0;char r=getchar();T neg=1;
while(r>'9'||r<'0'){if(r=='-')neg=-1;r=getchar();}
while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
x*=neg;
}
ll n,mod;
const int maxn=2e9+10;
const int maxm=1e9+10+10;
struct martix{
ll m[10][10];
void init(){clean(m,0);}
}start_;
inline martix mutiply(martix input1,martix input2,int a,int b,int c){
martix output;
output.init();
loop(i,1,a){
loop(j,1,b){
loop(k,1,c){
output.m[i][k]+=input1.m[i][j]*input2.m[j][k];
output.m[i][k]%=mod;
}
}
}
return output;
}
inline martix fastpower(martix a,int times){
martix stag=a;
martix res=start_;
while(times){
if(times&1)res=mutiply(res,stag,2,2,2);
times>>=1;
stag=mutiply(stag,stag,2,2,2);
}
return res;
}
int main(){
#ifndef ONLINE_JUDGE
//freopen("datain.txt","r",stdin);
#endif
read(n);
read(mod);
start_.init();
start_.m[1][1]=start_.m[2][2]=1;
martix ans;
ans.init();
ans.m[1][1]=2;ans.m[1][2]=1;ans.m[2][1]=1;ans.m[2][2]=1;
if(n<=3){
if(n==3)printf("2\n");
else printf("1\n");
}
else{
martix zhuanzhi;zhuanzhi.init();
zhuanzhi.m[1][1]=1;zhuanzhi.m[1][2]=1;zhuanzhi.m[2][1]=1;zhuanzhi.m[2][2]=0;
ans=mutiply(ans,fastpower(zhuanzhi,n-3),2,2,2);
printf("%lld\n",ans.m[1][1]);
}
return 0;
}
一般线性递推的答案矩阵和转移矩阵构造
- 观察递推式,看递推式中待求项和已知项之间的关系,如果待求项x要n个已知项yi来求的话,直接构造一个一行n列的答案矩阵,这样做的原因如下:
首先定义一个概念:层,对于一个线性递推等式,等式左边的项的层等于右边的项的层+1,如:$f[n]=f[n-1]+f[n-2]$,f[n]的层=f[n-1]的层+1/f[n-2]的层+1,那么显然有一个性质:
线性关系中,层数高的可以由层数低的”变换”而来,这个变换是指在低层项前乘上一个系数从而得到高层项
- 根据矩阵乘法的概念推出转移矩阵(见上文)
一些练习:(写出答案矩阵和转移矩阵,答案不唯一)
- $f[n]=f[n-1]+f[n-2]+n+1$
$$
\begin{pmatrix}
f[n-1] & f[n-2] & n & 1\
\end{pmatrix}
\times
\begin{pmatrix}
1 & 1 & 0 & 0\1 & 0 & 0 & 0\1 & 0 & 1 & 0\1 & 0 & 1 & 1
\end{pmatrix}
=\begin{pmatrix}
f[n] & f[n] & n+1 & 1\
\end{pmatrix}
$$
- $f[n]=A\times f[n-1]+B\times f[n-2]$
$$
\begin{pmatrix}
f[n-1] & f[n-2]\
\end{pmatrix}
\times
\begin{pmatrix}
A & 1\
B & 0\
\end{pmatrix}
=\begin{pmatrix}
f[n] & f[n-1]\
\end{pmatrix}
$$




