数学基础-概率和期望
高中部分的概率和期望知识总结
事件
事件
事件分为
必然事件
不可能事件
随机事件
基本事件(空间)
基本事件:不能够再分的事件,其他的事件都能够由基本事件来表示
基本事件空间:基本事件构成的集合,用大写希腊字母$\omega$表示
频率和概率
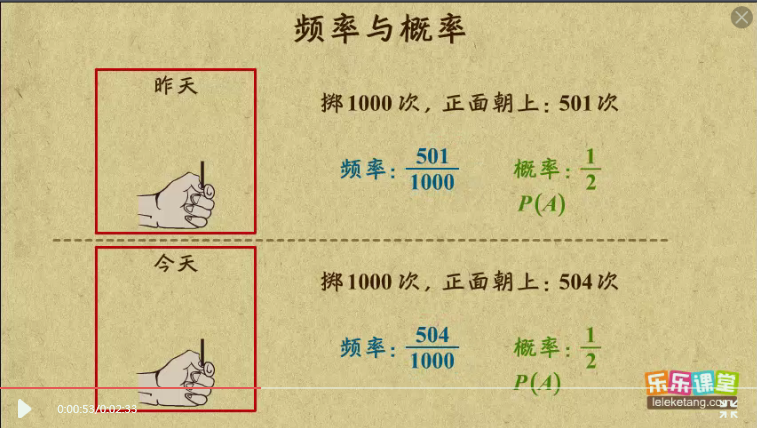
如图,概率是事件的基本性质,是不变的,而频率=$\frac{事件出现的次数(也叫事件的频数)}{总次数}$,是会改变滴
频率只能够近似的表示概率,但不等同!这就是你买1000个中奖率为千分之一的彩票而不中奖的原因了
概率范围:[0,1]
概率的性质
事件的关系
(此处省略包含,并事件,交事件的引入)
互斥事件:事件A和事件B互为互斥事件,当且仅当事件A和事件B不可能同时发生
对立事件:事件A和事件B互为对立事件,当且仅当事件A和事件B互为互斥事件且事件A和事件B的并集为整个基本事件空间,也就是要么发生A要么发生B,不可能发生C
概率运算
- 互斥事件的概率运算(即概率加法公式):
设事件A和事件B为互斥事件,概率分别为P(A),P(B),那么P(A∪B)=P(A)+P(B)
- 对立事件的概率
设事件A和事件B为对立事件,则P(A)+P(B)=1
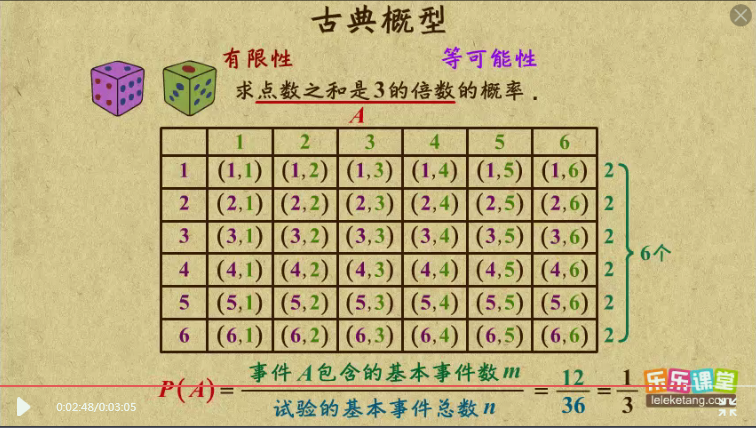
古典概型
定义
把具有有限性,等可能性的事件叫做古典概型
概率计算
$$P(A)=\frac{事件A包含的基本事件数m}{试验的基本事件总数n}$$
如:
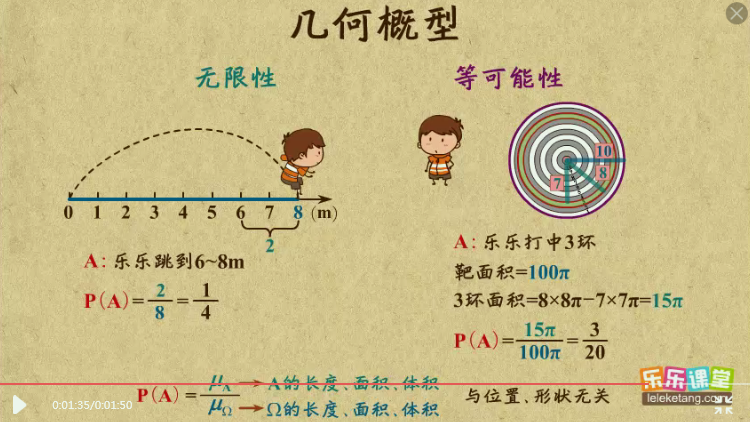
几何概型
把具有无限性,等可能性的事件叫做古典概型
概率计算
$$P(A)=\frac{A的长度,面积,体积\mu_A}{\omega的长度,面积,体积\mu_\omega}$$
如:
随机变量
定义
随机现象的结果对应的取值
对应扔色子来讲,随机变量X=1,2,3,4,5,6
分类
离散型随机变量
连续型随机变量
我们主要讨论离散型随机变量
离散型随机变量
定义
有限且可以枚举的随机变量
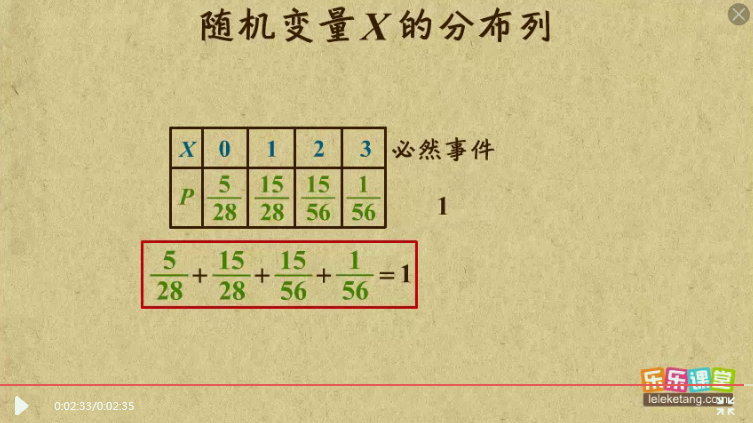
随机变量的分布列
把随机变量x的取值写在上面一行,其概率写在下面一行,这就叫做随机变量x的分布列
本质上就是一个表格:
| $x_1$ | $x_2$ | $\dots$ | $x_n$ |
|---|---|---|---|
| $P_{x_1}$ | $P_{x_2}$ | $\dots$ | $P_{x_n}$ |
- 性质:$\sum P_{x_i}=1$,也就是说分布列下面一行的所有值之和=1
如:
超几何分布
本质是不放回的取样,有公式可使用
具体细节留坑待补
相互独立事件
定义:结果互不影响的事件
概率计算:若A和B为相互独立事件,则$P_{(两者都发生)}=P(A)\times P(B)$
独立重复试验
定义
进行了多次试验,每次试验的条件都相同,各个试验当还相互独立,相关概率保持不变
其本质是有放回的取样


