第一届CSP-S复赛复习
是不是有点晚了?管那么多呢!
2019年11月11日15:34:08 鉴于今天上午考试爆炸,我提前开始写这篇博客.
复习什么呢?板子!当然更重要的是:遇到一题的时候的思维模式
一些语法
lowbit
lowbit(a)=a&(-a)板子
模拟退火
线段树
#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(int i=start;i<=end;i++)
#define ll long long
const int maxn=1000000+10;
ll data[maxn],sum[maxn<<2],lazy[maxn<<2];
int n,q;
void pushup(ll rt)
{
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void pushdown(ll rt,ll len)
{
if(!lazy[rt])return;
lazy[rt<<1]+=lazy[rt];
lazy[rt<<1|1]+=lazy[rt];
sum[rt<<1]+=lazy[rt]*(len-((len)>>1));
sum[rt<<1|1]+=lazy[rt]*(len>>1);
lazy[rt]=0;
}
void buildtree(ll l,ll r,ll rt)
{
lazy[rt]=0;
if(l==r)
{
sum[rt]=data[l];
return;
}
int m=(l+r)>>1;
buildtree(l,m,rt<<1);
buildtree(m+1,r,rt<<1|1);
pushup(rt);
}
void add(ll l,ll r,ll nl,ll nr,ll rt,ll num)
{
if(l<=nl&&nr<=r)
{
lazy[rt]+=num;
sum[rt]+=(nr-nl+1)*num;
return;
}
pushdown(rt,nr-nl+1);
int m=(nl+nr)>>1;
if(m<r)add(l,r,m+1,nr,rt<<1|1,num);
if(m>=l)add(l,r,nl,m,rt<<1,num);
pushup(rt);
}
ll query(ll l,ll r,ll nl,ll nr,ll rt)
{
if(l<=nl&&nr<=r)
{
return sum[rt];
}
pushdown(rt,nr-nl+1);
ll m=(nl+nr)>>1;
ll ans=0;
if(m<r)ans+=query(l,r,m+1,nr,rt<<1|1);
if(l<=m)ans+=query(l,r,nl,m,rt<<1);
return ans;
}
int main()
{
//freopen("datain.txt","r",stdin);
scanf("%d%d",&n,&q);
loop(i,1,n)scanf("%lld",&data[i]);
buildtree(1,n,1);
loop(i,1,q)
{
int op;
scanf("%d",&op);
if(op==1)
{
ll l,r,x;
scanf("%lld%lld%lld",&l,&r,&x);
add(l,r,1,n,1,x);
}
else if(op==2)
{
ll a,b;scanf("%lld%lld",&a,&b);
printf("%lld\n",query(a,b,1,n,1));
}
}
return 0;
}
exgcd 扩展欧几里得算法
模版:板子
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x=1,y=0;
return a;
}
int g=gcd(b,a%b,x,y);
int t=y;
y=x-a/b*y;
x=t;
return g;
}树链剖分
#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define anti_loop(i,start,end) for(register int i=start;i>=end;--i)
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define max(a,b) ((a>b)?a:b)
#define min(a,b) ((a<b)?a:b)
#define ll long long
const int maxn=1e5+10;
const int maxm=1e5+10;
int n,m,root,mod,cnt=0;
int num[maxn];
int head[maxn];
struct node{int e;int nxt;}edge[maxn<<1];
int dep[maxn],son[maxn],siz[maxn],fa[maxn];//x的深度,重儿子,子树点个数,父节点
int top[maxn],seg[maxn],rev[maxn];//x的重链头,在线段树中的位置,rev[x]指线段树中位置x对应的点
ll sum[maxn<<2],lazy[maxn<<2];
template<typename T>void read(T &x){
x=0;char r=getchar();T neg=1;
while(r<'0'||r>'9'){if(r=='-')neg=-1;r=getchar();}
while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
x*=neg;
}
inline void pushup(int rt){
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
inline void pushdown(int rt,int l,int r){
if(lazy[rt]){
lazy[rt<<1]+=lazy[rt],lazy[rt<<1|1]+=lazy[rt];
sum[rt<<1]+=lazy[rt]*(((l+r)>>1)-l+1);
//等价于lazy[rt]*(mid-l+1)
sum[rt<<1|1]+=lazy[rt]*(r-(((l+r)>>1)+1)+1);
//等价于lazy[rt]*(r-(mid+1)+1)
//这里注意加括号,否则优先级不正确代价很大
lazy[rt]=0;
}
}
void build(int l,int r,int rt){
if(l==r){
sum[rt]=num[rev[l]];
return;
}
int mid=((l+r)>>1);//注意大小于符号的方向!
build(l,mid,rt<<1);
build(mid+1,r,rt<<1|1);
pushup(rt);
}
ll query(int l,int r,int nl,int nr,int rt){
if(l<=nl&&nr<=r){
return sum[rt];
}
pushdown(rt,nl,nr);
int mid=(nl+nr)>>1;
ll _sum=0;
if(mid>=l)_sum+=query(l,r,nl,mid,rt<<1);
if(mid<r)_sum+=query(l,r,mid+1,nr,rt<<1|1);
return _sum;
}
void update(int l,int r,int nl,int nr,int rt,int w){
if(l<=nl&&nr<=r){
lazy[rt]+=w;
sum[rt]+=(nr-nl+1)*w;
return;
}
pushdown(rt,nl,nr);
int mid=(nl+nr)>>1;
if(mid>=l)update(l,r,nl,mid,rt<<1,w);
if(mid<r)update(l,r,mid+1,nr,rt<<1|1,w);
pushup(rt);
}
void dfs2(int u,int f){//第二个dfs维护出seg,rev,top三个数组
if(son[u]){//一定要先维护重儿子的标记,使得在线段树区间内重链连续排列
seg[son[u]]=++seg[0];
rev[seg[0]]=son[u];
top[son[u]]=top[u];
dfs2(son[u],u);
}
for(int i=head[u];i!=-1;i=edge[i].nxt){//维护完重儿子后再维护轻儿子
int v=edge[i].e;
if(!top[v]){//排除掉重儿子和父节点
seg[v]=++seg[0];
rev[seg[0]]=v;
top[v]=v;
dfs2(v,u);
}
}
}
void dfs1(int u,int f){//第一次dfs维护出fa,dep,siz,son四个数组
fa[u]=f;
dep[u]=dep[f]+1;
siz[u]=1;
son[u]=0;
for(int i=head[u];i!=-1;i=edge[i].nxt){
int v=edge[i].e;
if(v==f)continue;
dfs1(v,u);
siz[u]+=siz[v];
son[u]=((siz[v]>siz[son[u]])?v:son[u]);
}
}
inline void addl(int u,int v){
edge[cnt].e=v;
edge[cnt].nxt=head[u];
head[u]=cnt++;
}
inline void reply(){//回答函数
loop(i,1,m){
int op;read(op);
if(op==1){
int x,y,z;read(x),read(y),read(z);
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]<dep[fy])swap(fx,fy),swap(x,y);
update(seg[fx],seg[x],1,seg[0],1,z);
x=fa[fx],fx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
update(seg[x],seg[y],1,seg[0],1,z);
}
else if(op==2){
int x,y;read(x),read(y);ll res=0;
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]<dep[fy])swap(fx,fy),swap(x,y);
res+=query(seg[fx],seg[x],1,seg[0],1);res%=mod;
x=fa[fx],fx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
res+=query(seg[x],seg[y],1,seg[0],1);
printf("%lld\n",res%mod);
}
else if(op==3){
int x,z;read(x),read(z);
update(seg[x],seg[x]+siz[x]-1,1,seg[0],1,z);
}
else if(op==4){
int x;read(x);
printf("%lld\n",(query(seg[x],seg[x]+siz[x]-1,1,seg[0],1))%mod);
}
}
}
int main(){
#ifndef ONLINE_JUDGE
freopen("datain.txt","r",stdin);
#endif
clean(head,-1);clean(dep,0);clean(siz,0);clean(top,0);clean(sum,0);clean(lazy,0);
read(n),read(m),read(root),read(mod);
loop(i,1,n)read(num[i]);
loop(i,1,n-1){
int ui,vi;
read(ui),read(vi);
addl(ui,vi);
addl(vi,ui);
}
dfs1(root,0);
top[root]=root,seg[root]=1,rev[1]=root,seg[0]=1;
//由于dfs2中无法对根节点赋值,因此要在dfs2以前将根的三个参数全部赋值完毕
//seg[0]代表线段树中的点的个数
dfs2(root,0);
build(1,seg[0],1);
reply();
return 0;
}
线性筛
int prime[maxn],cnt=0;
int v[maxn];//v[i]意思就是i的最小质因子
inline void shai(int n){
clean(prime,0);
clean(v,0);
cnt=0;
loop(i,2,n){
if(!v[i]){//若i是质数,记录
prime[++cnt]=i;
v[i]=i;
}
loop(j,1,cnt){
//对i乘上一个质因子prime[j],要保证这个质因子是i*prime[j]的最小质因子
//(其实就是尝试用i和prime[j]组合成一个数)
if(i*prime[j]>n||v[i]<prime[j])break;
//如果i的最小质因子比prime[j]小,那么就不用再乘了
v[i*prime[j]]=prime[j];
//否则记录
}
}
} Splay
手写版本
#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define ll long long
const int maxn=100000+10;
const int INF=1e9+7;
template<typename T>void read(T &x){
x=0;char r=getchar();T neg=1;
while(r>'9'||r<'0'){if(r=='-')neg=-1;r=getchar();}
while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
x*=neg;
}
struct node{
int f;
int siz;
int cnt;
int son[2];
int w;
}tree[maxn];
int numofp=0,root=0;
inline int getpos(int x){return ((tree[tree[x].f].son[0]==x)?0:1);}
inline void update(int x){tree[x].siz=tree[tree[x].son[0]].siz+tree[tree[x].son[1]].siz+tree[x].cnt;}
inline void Ro(int x){
int f=tree[x].f;
int ff=tree[f].f;
int s=tree[x].son[(getpos(x)==0)?1:0];
int posx=getpos(x);
int posf=getpos(f);
tree[f].son[posx]=s;
tree[s].f=f;
tree[ff].son[posf]=x;
tree[x].f=ff;
tree[x].son[posx^1]=f;
tree[f].f=x;//same!
update(f),update(x);
}
inline void Splay(int x,int to=0){
while(tree[x].f!=to){
int f=tree[x].f,ff=tree[f].f;
if(ff!=to){
if(getpos(f)==getpos(x))Ro(f);
else Ro(x);
}
Ro(x);
}
if(to==0)root=x;
}
inline void in(int w){
int _p=0;int cur=root;
while(cur&&tree[cur].w!=w)_p=cur,cur=tree[cur].son[w>tree[cur].w];
if(cur)tree[cur].cnt++;
else{
cur=++numofp;
tree[cur].cnt=1;
tree[cur].w=w;
tree[cur].siz=1;
tree[cur].son[1]=tree[numofp].son[0]=0;
tree[cur].f=_p;
if(_p)tree[_p].son[w>tree[_p].w]=cur;
}
Splay(cur);
}
inline void _find(int _w){
int cur=root;
while(tree[cur].w!=_w&&tree[cur].son[tree[cur].w<_w])
cur=tree[cur].son[tree[cur].w<_w];
Splay(cur);
}
inline int getrank(int _w){
_find(_w);
if(tree[root].w<_w)return tree[tree[root].son[0]].siz+tree[root].cnt+1;
else return tree[tree[root].son[0]].siz+1;
}
inline int _findKth(int _x){
int cur=root;
int _rank=_x;
while(1){
if(_rank<=tree[tree[cur].son[0]].siz)cur=tree[cur].son[0];
else if(_rank<=tree[tree[cur].son[0]].siz+tree[cur].cnt)return cur;
else _rank-=tree[tree[cur].son[0]].siz+tree[cur].cnt,cur=tree[cur].son[1];
}
}
inline int pre(int _w){
_find(_w);
if(tree[root].w<_w)return root;
int cur=tree[root].son[0];
while(tree[cur].son[1])cur=tree[cur].son[1];
return cur;
}
inline int bac(int _w){
_find(_w);
if(tree[root].w>_w)return root;
int cur=tree[root].son[1];
while(tree[cur].son[0])cur=tree[cur].son[0];
return cur;
}
inline void del(int _w){
int fr=pre(_w),ba=bac(_w);
Splay(fr);Splay(ba,fr);
int _del=tree[ba].son[0];
if(tree[_del].cnt>1)--tree[_del].cnt,Splay(_del);
else tree[ba].son[0]=0;
}
int main(){
register int n;read(n);
register int opt,x;
in(INF);
in(-INF);
loop(i,1,n){
read(opt);read(x);
if(opt==1)in(x);
else if(opt==2)del(x);
else if(opt==3)printf("%d\n",getrank(x)-1);
else if(opt==4)printf("%d\n",tree[_findKth(x+1)].w);
else if(opt==5)printf("%d\n",tree[pre(x)].w);
else if(opt==6)printf("%d\n",tree[bac(x)].w);
}
return 0;
}
STL版本
#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define anti_loop(i,start,end) for(register int i=start;i>=end;--i)
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define max(a,b) ((a>b)?a:b)
#define min(a,b) ((a<b)?a:b)
#define ll long long
template<typename T>void read(T &x){
x=0;char r=getchar();T neg=1;
while(r>'9'||r<'0'){if(r=='-')neg=-1;r=getchar();}
while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
x*=neg;
}
int n;
int main(){
read(n);
register int op,x;
vector<int>vec;
loop(i,1,n){
read(op);
read(x);
if(op==1)
vec.insert(lower_bound(vec.begin(),vec.end(),x),x);
else if(op==2)
vec.erase(lower_bound(vec.begin(),vec.end(),x));
else if(op==3)
printf("%d\n",lower_bound(vec.begin(),vec.end(),x)-vec.begin()+1);
else if(op==4)
printf("%d\n",vec[x-1]);
else if(op==5)
printf("%d\n",vec[lower_bound(vec.begin(),vec.end(),x)-vec.begin()-1]);
else
printf("%d\n",vec[upper_bound(vec.begin(),vec.end(),x)-vec.begin()]);
}
return 0;
}LIS,LCS
小学奥数题&思维题
例题:noip 2012 D1T1 luogu P1079 Vigenère 密码
不要去傻傻的打表,去发现这个大表里面的公式.(当然如果降智降得厉害,打表也不是不行)
这题真的是…..一言难尽,尝试打表吧,证明不出来的
(不)基础算法
模拟
例题:【noip 2015 D1T1】P2615 神奇的幻方
模拟即可
大模拟..
随机化
这是个好东西,但是慎用
模拟退火!,记得看一下,骗分利器!
模拟退火模版题
例题:noip 2012 Day2 T2 P1080 国王游戏
根本不会猜贪心的蒟蒻只能够用随机化了,能够水60分呢
hash
记得复习!
搜索
数独,让人自闭的码农题,不想说了
关键是剪枝,使用了放缩法剪枝!(感觉自己一辈子都用不来的东西)
搜索+剪枝
爆搜啊
例题:luogu P1118 [USACO06FEB]数字三角形Backward Digit Su…
杨辉三角(组合数)加速搜索
记忆化搜索
例题:【noip 2015 Day1 T3】luogu P2668 斗地主
这搜索是真的煎熬..
BFS染色
例题:[USACO08FEB]流星雨Meteor Shower
BFS搜索即可
宽搜,注意对弹簧的判断
思路很简单,可以看看
注意搜索顺序
这题输入非常鬼畜
迭代加深,这是个好东西,记得复习!
二分
关键是发现其中的单调性.其实大部分的二分都是这样
可以用分层图解决,但是也可以二分套spfa,是一个经典模型了
01分数规划
一般遇到题就想办法去抽象出这个模型就可以了.而且一般来讲,这种算法只能够求最优比率
最好在考前手推一下这些个题
例题们:
luogu P4377 [USACO18OPEN]Talent Show
luogu P2868 [USACO07DEC]观光奶牛Sightseeing Cows
差分
一阶差分+线段树
二阶差分!
例题:LOJ #10131. 「一本通 4.4 例 2」暗的连锁
树上差分好题一枚.将每条主要边的权值定义为经过它的附加边的条数,这样一来就可以枚举每一条主要边然后得解了
例题:luogu P3128 [USACO15DEC]最大流Max Flow(树上差分之点差分板子题)
树上差分模版,点差分
DP(动态规划)
线性DP
NOIP2018道路铺设:
对于第i个坑,要么被前面的一起填掉,要么自己还要新开一个坑,于是设高度d,分类讨论:
$$
f[i]=\begin{cases}
f[i-1] \ (d[i-1]<=d[i])\f[i-1]+d[i-1]-di
\end{cases}
$$
例题:「一本通 6.2 练习 2」[USACO08DEC] Patting Heads 轻拍牛头
这题关键是要注意到能够被整除的数之间的关系
这题还比较值得研究,其中的划分形DP和去重的处理都很有借鉴意义
状态设计来自于答案,考虑转移的时候尝试考虑决策或”考虑最后一步”即可找出方程然后AC
一个有效的经验:数组无序的时候,进行等效的排序,状态设计仍然来自于答案,考虑转移的时候仍然尝试考虑决策
很简单的暴力DP,状态设计仍然来自于答案…(省略几个字)..但是暴力DP现在luogu上不能拿满分了
仍然秉承上面的原则就可以做出这题
继续秉承上面的原则就可以做出这题
仍然继续秉承上面的原则就可以做出这题
例题:luogu P1439 【模板】最长公共子序列——【LIS的nlogn解法详解】
是一个很好的利用离散化的例子,可以复习一下
比较经典的模型:求一个序列中两个不相交连续的子序列的最大和,利用了前缀和和后缀和思想解题
棋盘DP
棋盘DP,统计最短路条数
例题:noip 2008 T3 luogu P1006 传纸条
棋盘DP,可以复习一下
好像是和前面这题神似呢
有时候有一些题看上去可以用搜索,但实际上只能够使用棋盘DP来解决,这里列出来的棋盘DP大都是这个样子
数位DP
这个考试遇到了只有狗带的份
区间DP
树形DP
但是树形DP还是学的巨水无比
状态压缩DP
二进制状压一般用作表示集合中元素的选取情况,使用条件(特征)是$2^n$比较小(考到3进制状压算我倒霉好吧)
状压DP入门之一
一道经典状压DP,注意状态的设计和很多细节
一道不错的状压题目,核心仍然是利用状态压缩在表示集合的选取然后进行DP
例题:luogu P4363 [九省联考2018]一双木棋chess
这是我做到的比较好的一题了.这题的关键是想到可以用一条从左下到右上的对角线来表示当前棋盘的状态
背包
这题依赖的物品数比较少,因此可以用分组背包来解决,就懒得去打一个树形DP了
二维费用背包模版题(都快忘了,记得复习)
例题:luogu P2918 [USACO08NOV]买干草Buying Hay
完全背包(非模版)+估计上限
二进制拆分对混合背包非常有效!
资料:背包问题详解!
树形DP
luogu P2986 [USACO10MAR]伟大的奶牛聚集Great Cow Gat…
树的重心,重点,记得复习!
树的重心和最小生成树的综合
字符串算法
这个考到了基本上$CSP$就没了
字典树
巧妙的使用字典树避免了DP的各种煞笔细节(字典树还是可以看一下的)
manacher算法
有时间就去看下吧(估计也不会去看~~)
KMP
就这样了,不敢再说什么了
AC自动机
不要去想了~~
图论
强连通分量SCC
一般来讲,考scc的题都是要分析联通性和scc里面的某些特殊性质的
认真读题后发现是个模版
认真读题后也发现是个模版
例题:loj #10094. 「一本通 3.5 练习 2」消息的传递
裸模版题
例题:luogu P2341 [HAOI2006]受欢迎的牛
关键是要分析出来连接关系
例题:P2921 [USACO08DEC]在农场万圣节Trick or Treat on the Farm
这题乍一看不是很简单,实际上分析出scc里面的性质:一个奶牛获得的糖果数等于其所在scc的点的糖果总数,就是一道模版题罢了
tarjan+贪心
缩点后树形DP(树形DP学的太菜,走了~~)
例题:luogu P2746 #10093. [USACO5.3]校园网Network of Schools
需要稍加分析,得出结论答案为入度和出度的差
例题:loj #10092 luogu P2272 [ZJOI2007]最大半连通子图
这题主要是太多数学符号了,看得人眼花缭乱的.其实不算特别难
例题:loj #10096 luogu P3627 [APIO2009]抢掠计划
tarjan+spfa/拓扑排序,收集在我的luogu题库里面的一道模版题
MST问题(最小生成树)
例题:luogu P2330 [SCOI2005]繁忙的都市
稍加分析后可以发现本题就是求一个MST
不断加边的kruskal
树链剖分
这个东西,板子还比较熟练,但是做过的题少有比较好的呢
模版
模版
例题:luogu P3038 [USACO11DEC]牧草种植Grass Planting
边权转点权的树链剖分
边权转点权的树链剖分
例题:luogu P2146 [NOI2015]软件包管理器
这是一个比较好的树链剖分题了.要分析出依赖关系从而得到操作的本质和树链剖分支持的操作的关系
可以用树上差分做,同时可以用树剖.
树链剖分求lca
关键是一个很好的性质:某一条路径起点和终点的LCA被包含在另外一条路径上,可反证证明
最短路
关键是意识到两个角色的等价性以及拥有大力分类讨论的意识,入手点为考虑路径可能经过的点的情况
关键是能够知道出现了乘法,我们可以用对数来将其转化为加法
例题:UVA10537 The Toll! Revisited
秉承正难则反的原则,反向跑最短路,再加一点分类讨论即可
例题:It’s not a Bug, it’s a Feature! UVA - 658
用状态压缩来表示bug的有无(0没有,1有),然后就可以把每个bug的状态表示的数看做点,然后就可以从(11111…111)开始,枚举每一个补丁(lrj大佬说这叫做隐式图搜索),判断并且进行状态转移
例题:P2176 [USACO14FEB]路障Roadblock
暴力即可
最短路计数,经典问题了.不要忘了怎么转移数量的!最好考前看看(最短路计数模版)
本是DP,但是是可以转化为图论模型的,值得借鉴的一个思路
例题:luogu P1339 [USACO09OCT]热浪Heat Wave
模版
例题:P2850 [USACO06DEC]虫洞Wormholes
spfa判负环,模版记得复习!
分层图最短路
例题们:
luogu P4011 孤岛营救问题 #10073. 「一本通 3.2 例 2」拯救大兵瑞恩
luogu P3119 [USACO15JAN]草鉴定Grass Cownoisseur
最短路树(图)
例题:UVA1416 Warfare And Logistics
利用最短路图优化的暴力,因为删除的边如果不在最短路图上,那么整个图中不会有某个点的最短路数组dis[i]被改变
例题:UVA10917 Walk Through the Forest
可以从最短路图的角度去理解,还可以直接暴力理解~~
例题:CF1005F Berland and the Shortest Paths
最短路(图)树有很多很好的性质,其中之一就体现在这个题里面.我们也许可以尝试去往题里面套算法?,利用反证法可以得出最短路图就是本题的最优答案
差分约束
考前好好看看
例题们:
「一本通 3.4 例 1」 POJ 1201-Intervals
luogu P3084 [USACO13OPEN]照片Photo
次短路
例题:luogu P2865 [USACO06NOV]路障Roadblocks
重要模型!考前看一看其中的分类讨论
Floyd
loop(k,1,n)
loop(i,1,n)
loop(j,1,n)这三行代码就是这个算法的核心,其中第一行代码可以大改
传递闭包
例题:POJ 1094_Sorting It All Out
这是一道实现起来很恶心的题.关键是把不等关系转化为一个二维数组,利用传递闭包来得到关系长度大于1的点之间的关系
最短路&最长路
入手点和前面那道密室有点像,都是对最后的答案——在这里就是添加的那条边引起的变化——大力讨论(其实这题讨论不算大力),然后得到相应的答案
关键是:动态又具有一定单调性限制的最短路就要考虑Floyd,这时我们是通过修改Floyd最外层的循环得到解的
例题:P2888 [USACO07NOV]牛栏Cow Hurdles
稍微改一下方程即可
Floyd和矩阵快速幂
例题:poj3613 ACwing 345:Cow Relays–牛站
Floyd和矩阵有着千丝万缕的联系,而矩阵又和快速幂有着说不清道不明的关系,于是Floyd和矩阵快速幂就有千丝万缕的说不清道不明的关系了
关键是推导出这个广义的矩阵乘法满足分配率,于是就可以把矩阵乘法替换成”广义矩阵乘法”
Floyd求无向图最小环
例题:一本通 3.2 例 1 Sightseeing Trip
枚举一个k和和它相邻的两个点,看这三个点能否构成一个最小环,具体实现看代码
建图技巧
虚点连边
虚点连边是一种很有效的优化建边复杂度的方式
Part1
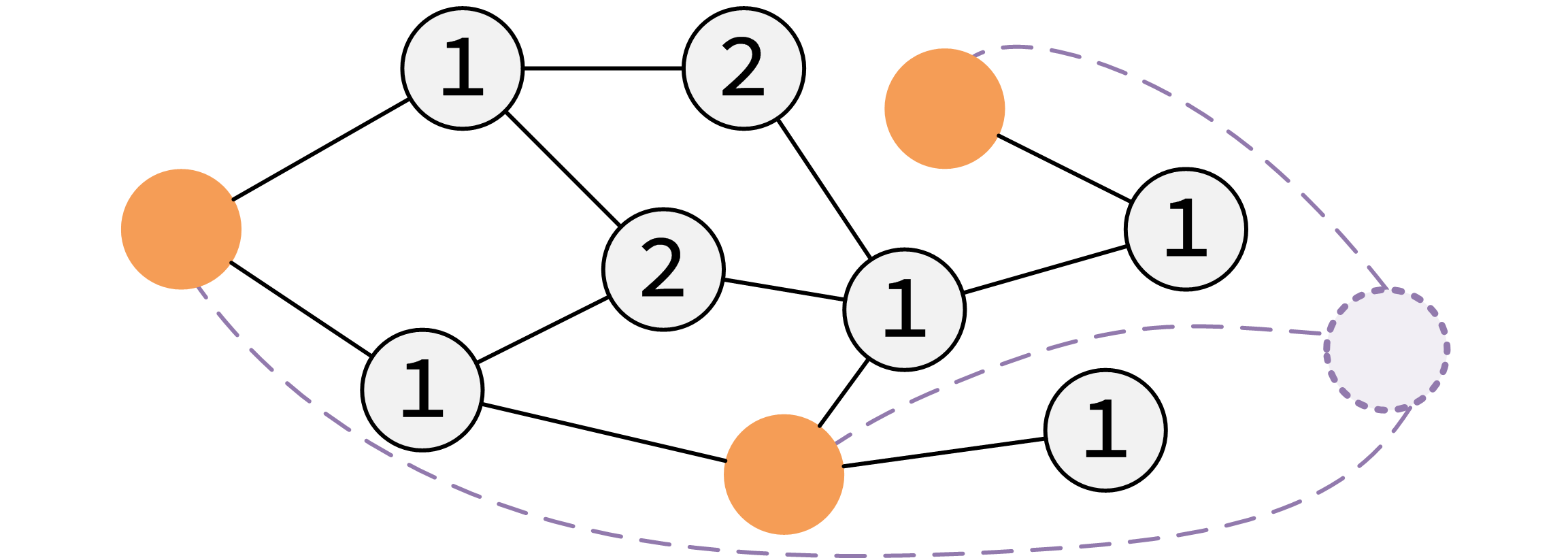
我们可能会遇见这样一种题,给你几个点,其他的点离这些给出的点的最近距离是多少。
我们可以对于每一个点进行最短路,但似乎这样并不是很好操作。
我们可以自己给出一个点,然后向每个被标记的点连一条单向边,这样就只需要进行一次最短路就可以了。
举个例子,橙色为标记点,数字为最近距离。
Part2
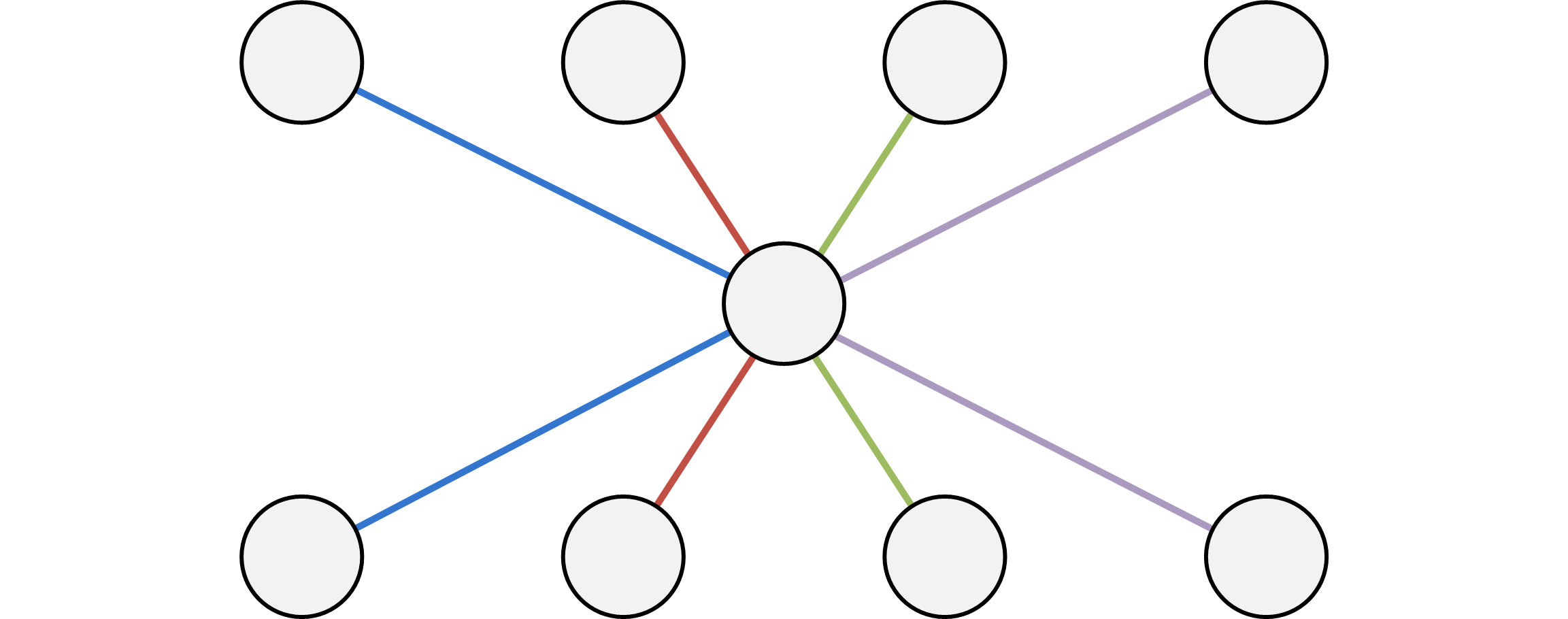
如果对于两个点集A和B,你需要对A中的每一个点向B中的每一个点都建一条边,如果直接操作,复杂度很明显是 $O(n^2)$的,有没有更快的方法呢?
我们可以建一个虚点P,然后对A里的每一个点向P连一条单向边边,然后对P向B中的每一个点建一条单向边,这样只需要$O(2n)$ 的复杂度就可以完成了。
网络流
没得搞,不会.
数据结构
并查集
一类题:并查集求连通块
例题:【noip 2015 D1T2】luogu P2661 信息传递
并查集求最小环!经典模型,记得复习
也可以搜索,但是用并查集实现会更加简单
单调数据结构
有了单调性,我们就可以很容易的(一般是$O(1)$)的取出某个集合里的最值
单调栈
例题:mzojP1419 浇水
单调栈的模版题(但是我都快忘了!),复习.
单调队列
经典的模版
单调队列模版,滑动窗口的形式化描述.
这一题的关键是发现:先被切的蚯蚓中的相应段总是比后被切的蚯蚓中的相应段长这一单调性.
本题十分经典,求长度不超过m的最大子序列和.关键是把最大子序和用前缀和的形式表达出来,然后对于每一个位置找前面的最小的前缀和,从而转化成单调队列的模版题.
单调队列优化DP
单调队列优化DP使用的条件是:
- 最优化(min,max等)
- 对象变量的取值范围单向变化(上下界一起向上或向下)
一般的分析步骤:
- 分析对象变量的取值范围
- 分析单调队列中的决策的单调性
具体见上面的链接+这个链接
带根号的数据结构
莫队
这可是号称可以解决任何区间问题的算法!优美的暴力,为了骗分最好还是看一下!
莫队模版
例题:luogu P1972 [SDOI2009] HH的项链
奇偶优化模版(当然现在在luogu上也过不了了)
带对数的数据结构
线段树
例题:luogu P5097 [USACO2004OPEN]Cave Cows 2 洞穴里的牛之二
模版题
例题:luogu P2824 [HEOI2016/TJOI2016]排序
这题主要是要发现对一个01序列的排序可以用log级别的线段树来操作,也就是统计区间的和,然后把前面的赋值为0,后面的赋值为1就行了,本质上是一个区间修改+单点查询的线段树
经典的乘法线段树,记得看看!
好题一枚!关键是离散化和考虑维护的值
关键是发现:一个区间的结尾必定对应一个在其前面的开头.若我们查询到这个询问的右界的左边[0,R]有x个地雷区间的开头,左界的左边[0,L-1]有y个地雷区间的结束,由于一个区间的结尾必定对应一个在其前面的开头,故区间[L,R]中颜色的个数就等于x-y,类似于差分的思想
例题:luogu P2574 XOR的艺术 P3870 [TJOI2009]开关
和异或相关的位运算.由于异或的封闭性,考虑用lazy标记来保存一个区间被异或的情况.由于一个区间里面的0和1的个数是可以用区间和求出来的,因此这个题就可以只维护一个区间和,也就是一个区间修改和查询的线段树,只是lazy标记有点不一样
看似要动态开点,实际上可以预先开够空间,然后直接加就行
例题:noip 2012 提高组 Day2 T2 LuoguP1083 借教室
按照时间来建线段树(有一丢丢线段树分治的味道)
线段树分治
基本思想就是:离线询问,按照时间顺序建线段树,每个节点要保存影响,然后最后一遍dfs求出所有询问,(但是感觉考场上想得出来也不一定打得出来~~)
平衡树
例题:luogu P2286 [HNOI2004]宠物收养场
模版题..
例题:luogu P2234 [HNOI2002]营业额统计
稍加分析就知道是一道模版题
例题:luogu P1486 [NOI2004]郁闷的出纳员
乍一看以为要写一个区间修改,但实际上只需要保存一个全局变量表记录工资变化量,之后的员工就直接加上这个变化量就可以了
数学
数论
关键是要知道唯一分解定理及其推论,然后可以了解一下分治求等比数列,这个题可以好好康康
中国剩余定理模版****,考前记得复习!
例题:「一本通 6.2 练习 5」luoguP1445 [Violet]樱花
这是一道狗粮题.关键是会推式子!这个题的推导过程比较有意思,可以看看(好像链接里的推导有一点点不影响结果的小错误)
例题:「一本通 6.2 例 1」 UVA10140 Prime Distance[线性筛]
基本思想是变相打表,也就是不把所有的表打完,而只打一部分,利用这一部分来取得我们需要的另外一部分
例题:「一本通 6.3 例 1」luogu P1463 [POI2002][HAOI2007]反素数
答案肯定是在小于n里面的因数个数最大的数中最小的一个,因此根据唯一分解定理,爆搜即可,数据范围有保障的
例题:「一本通 6.4 例 1」 luogu P1516 青蛙的约会
可以把两只青蛙的位置转化为同余意义下的式子,因此可以列出等式从而求解
中国剩余定理的模版,记得看看!
乘法逆元的模版,这个比较熟了
资料:数论锦集!
计算几何
这个考到了只有持矢
例题:P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows
二维凸包$CSP$可能会考吗?估计不会,反正考到只有凉凉
例题:luogu P1452 Beauty Contesthttps://blog.csdn.net/weixin_43907802/article/details/89071224
话说这是另外一个叫做$Andrew$的大佬发明的算法,叫做$Andrew$算法呢
线性基
*模版:*luogu P3812 【模板】线性基
这个还是和xyx一起学的,但我敢保证我们两个现在都忘了这东西怎么实现了
初级线性代数
矩阵
矩阵加速递推式,主要是要会构造矩阵.会构造转置矩阵后,使用矩阵快速幂就可以解决问题了(矩阵乘法完美满足结合律!)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,mod=1e9+7;
ll k;
const int maxn=100+5;
struct martix
{
ll m[maxn][maxn];
}e;
inline ll read()
{
ll ans=0;
char r=getchar();
while(r<'0'||r>'9')r=getchar();
while(r>='0'&&r<='9')
{
ans=ans*10+r-'0';
r=getchar();
}
return ans;
}
martix datasetting()
{
martix x;
n=read();scanf("%lld",&k);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
x.m[i][j]=read();
return x;
}
martix mut(martix a,martix b)
{
martix ans;
memset(ans.m,0,sizeof(ans.m));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int p=1;p<=n;p++)
ans.m[i][j]=ans.m[i][j]%mod+a.m[i][p]*b.m[p][j]%mod;
return ans;
}
void printans(martix x)
{
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
printf("%lld ",x.m[i][j]%mod);
printf("\n");
}
}
void fastpower(martix x,ll t)
{
martix wei=x;
martix res=e;
while(t)
{
if(t&1)res=mut(res,wei);
wei=mut(wei,wei);
t>>=1;
}
printans(res);
}
int main()
{
martix xx=datasetting();
for(int i=1;i<=n;i++)
e.m[i][i]=1;
fastpower(xx,k);
return 0;
}
/********************************************************************
ID:Andrew_82
LANG:C++
PROG:fast power
********************************************************************/
概率期望
期望的定义是$\sum P_i\times W_i$
根据定义dfs,记录距离和概率,最后相加就行
这题有两个难点:根据组合数公式列出主队赢球的概率式子,发现这个式子是可以O(n)递推的
期望DP
需要知道期望的线性性,也就是期望是可以掰开递推的.具体看博客吧(DP方程太长不好搬运).至于如何掰开,就是强行掰开啊!!
最后的最后
update 2019年12月1日12:00:14
以上的复习内容基本没有压中这次CSP-S的考点,因此,显而易见的,Andrew光荣的省三退役了(虽然成绩还没有出来,但结果是可以预料的)
这几天的常规学习日子真是不好过啊,毕竟要2个月学完一学期的课程,这工作量不是开玩笑的.
对了,前几天看到一个同学写的退役记,我觉得写的很有水平呢 这里是传送门!


