数列递推:不定点法和特征方程法
数列递推形式
不动点法
使用条件
分式线性:$a_{n+1}=\frac{pa_n+q}{ra_n+s}$
内容
不动点:对于如上这个没有初值的数列,当数列中任意一个数取到某一个值$\lambda$的时候,这个数列的每一项都相等,也就是$a_{n+1}=a_n$,这个时候我们把这个$\lambda$叫做不动点
当不动点$\lambda_1!=\lambda_2$时,数列$\frac{a_{n}-\lambda_1}{a_{n}-\lambda_2}$是等比数列
当$\lambda_1=\lambda_2$时,数列$b_n=\frac{1}{a_n-\lambda}$是等差数列
原理
- 核心思想:利用不动点的特殊性质将上式转为等比或等差数列
- 推导过程
假设出我们的参数$\lambda$,接下来我们会证明这样一个性质:
$\lambda$满足
$$a_{n+1}-\lambda=\frac{(p-\lambda r)(a_n-\lambda)}{ra_n+s}$$
证明:
将上式左右两边都减去这个参数得到:
$$a_{n+1}-\lambda=\frac{pa_n+q}{ra_n+s}-\lambda=\frac{pa_n+q-\lambda ra_n-\lambda s}{ra_n+s}=\frac{(p-\lambda r)a_n+q-\lambda s}{ra_n+s}$$
如果想要上式的等号左边和等号右边的分子成
$$a_{n+1}-\lambda=\frac{(p-\lambda r)(a_n-\lambda)}{ra_n+s}$$
的形式,那么就有关系:
$$(q-\lambda s)=(p-\lambda r)(-\lambda)$$
(这个式子的含义是$(q-\lambda s)$是$(-\lambda)$的$(p-\lambda r)$倍,带回式子中发现,如果有$\lambda$满足这个条件,一定可以化成上面我们想象的那种形式)
也就是
$$q-\lambda s=\lambda ^2 r-p\lambda$$
$$r\lambda^2+(s-p)\lambda-q=0$$
而根据不动点的定义有:
$$\lambda=\frac{p\lambda+q}{r\lambda+s}$$
$$\lambda(\lambda+s)=p\lambda+q$$
$$r\lambda ^2+s\lambda-p\lambda-q=0$$
我们发现上面的两个方程是一样的,因此不动点$\lambda$就有
$$\lambda=\frac{p\lambda+q}{r\lambda +s}<=>(q-\lambda s)=(p-\lambda r)(-\lambda)$$
所以向$a_{n+1}-\lambda=\frac{(p-\lambda r)a_n+q-\lambda s}{ra_n+s}$代入$(q-\lambda s)=(p-\lambda r)(-\lambda)$得
$$a_{n+1}-\lambda=\frac{(p-\lambda r)(a_n-\lambda)}{ra_n+s}$$
证毕
从上面的证明我们可以看出,不动点$\lambda$可能有两种情况:有两个解/一个解(在复数范围内),那么我们接下来就会证明如下结论:
$\lambda_1!=\lambda_2$时,数列$\frac{a_{n}-\lambda_1}{a_{n}-\lambda_2}$是等比数列
$\lambda_1=\lambda_2$时,数列$b_n=\frac{1}{a_n-\lambda}$是等差数列
- 当$\lambda_1!=\lambda_2$
我们将他们分别带回我们开始的$a_{n+1}-\lambda=\frac{(p-\lambda r)(a_n-\lambda)}{ra_n+s}$中有:
$$a_{n+1}-\lambda_1=\frac{(p-\lambda_1 r)(a_n-\lambda_1)}{ra_n+s}\a_{n+1}-\lambda_2=\frac{(p-\lambda_2 r)(a_n-\lambda_2)}{ra_n+s}$$
两式相除得到:
$$\frac{a_{n+1}-\lambda_1}{a_{n+1}-\lambda_2}=\frac{(p-\lambda_1 r)(a_n-\lambda_1)}{(p-\lambda_2 r)(a_n-\lambda_2)}$$
$$\frac{a_{n+1}-\lambda_1}{a_{n+1}-\lambda_2}=\frac{(p-\lambda_1 r)}{(p-\lambda_2 r)}\times \frac{(a_n-\lambda_1)}{(a_n-\lambda_2)}$$
因此:
$$\frac{a_{n}-\lambda_1}{a_{n}-\lambda_2}=[\frac{(p-\lambda_1 r)}{(p-\lambda_2 r)}]^{n-1}\frac{(a_1-\lambda_1)}{(a_1-\lambda_2)}$$
于是就可以反过来解出原来的通项公式:
令$t=[\frac{(p-\lambda_1 r)}{(p-\lambda_2 r)}]^{n-1}\frac{(a_1-\lambda_1)}{(a_1-\lambda_2)}$
$$a_n=\frac{\lambda_1-t\lambda_2}{1-t}$$
- 当$\lambda_1=\lambda_2=\lambda$
则有:
$$a_{n+1}-\lambda=\frac{(p-\lambda r)(a_n-\lambda)}{ra_n+s}$$
$$\frac{1}{a_{n+1}-\lambda}=\frac{ra_n+s}{(p-\lambda r)(a_n-\lambda)}$$
令$b_n=\frac{1}{a_n-\lambda}$,则$a_n=\frac{1}{b_n}+\lambda$
$$b_{n+1}=\frac{ra_n+s}{(p-\lambda r)}b_n=\frac{r(\frac{1}{b_n}+\lambda)+s}{(p-\lambda r)}b_n=\frac{r+r\lambda b_n+sb_n}{(p-\lambda r)}\=\frac{r}{(p-\lambda r)}+\frac{r\lambda +s}{p-\lambda r}b_n$$
因为$\lambda$是方程$r\lambda^2+(s-p)\lambda-q=0$的唯一根,那么$2\lambda=\frac{(p-s)}{r},\lambda=\frac{p-s}{2r}$
代入$b_{n+1}$中得到
$$b_{n+1}=\frac{r}{p-\frac{p-s}{2}}+b_n=\frac{2r}{p+s}+b_n$$
因此$b_n$是等差数列
例题
设无穷项数列 $a_n$ 满足 $a_{n+1}a_n+3a_{n+1}+a_n+4=0$,若$a_{2016}$是$a_n$的最小项,则$a_1$的取值范围是?
转化为分式形式:$a_{n+1}=-\frac{a_n+4}{a_n+3}$
求出不动点$\lambda=-2$
构造等差数列:
$$a_{n+1}+2=-\frac{a_n+4}{a_n+3}+2=\frac{a_n+2}{a_n+3}$$
$$\frac{1}{a_{n+1}+2}=\frac{a_n+3}{a_n+2}=\frac{1}{a_n+2}+1$$
于是就有
$$\frac{1}{a_n+2}=\frac{1}{a_1+2}+n-1$$
观察此式,其中如果$a_1+2>0$,那么$a_n$将是一个恒大于零的递减数列,不存在某一项为最小值.但如果$a_1+2<0$,那么$\frac{1}{a_n+2}$是一个递增数列.如果用反比例函数来解释这个东西就是这样:
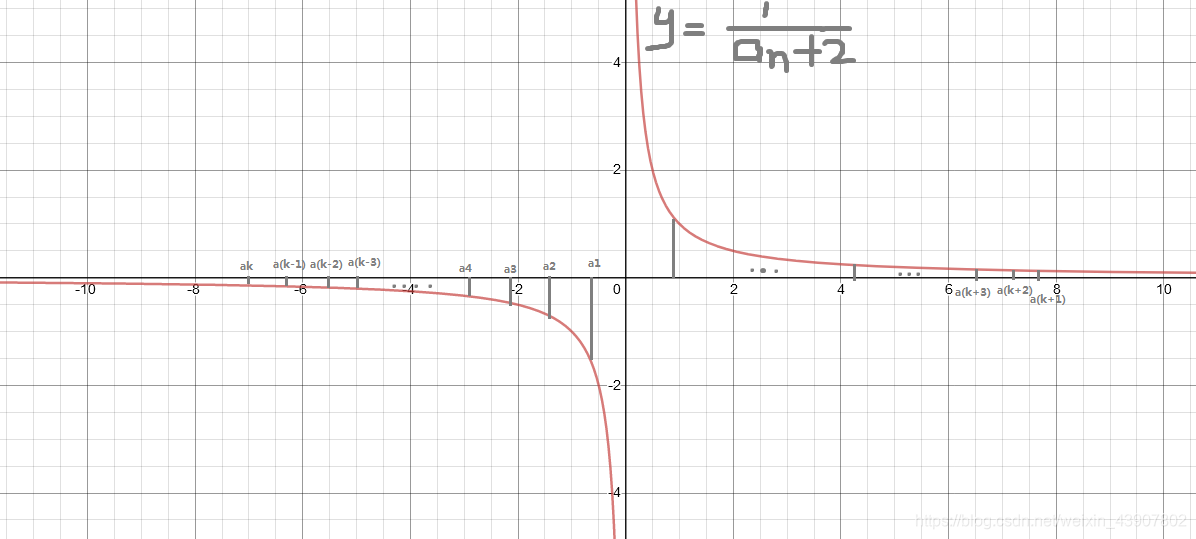
(图稍微画的有点问题,但影响不大)
其中$\frac{1}{a_1+2}<\frac{1}{a_2+2}<…<\frac{1}{a_k+2}<0<\frac{1}{a_{k+1}+2}<\frac{1}{a_{k+2}+2}…$
那么我们不难发现,此时数列$a_n$的最小值就对应着$\frac{1}{a_n+2}$的最后一个负数值
因此:
$$\begin{cases}\frac{1}{a_{2016}+2}<0\\frac{1}{a_{2017}+2}>0\end{cases}$$
解得$a_1\in(-\frac{4031}{2015},-\frac{4033}{2016})$
数列$x_n$满足$x_1=1,x_{n+1}=\frac{3+3x_n}{3+x_n}$,则数列的极限是?
方法一:无脑暴算
首先一波暴算得到不动点为$\lambda_1=-\sqrt 3,\lambda_2=\sqrt 3$,然后求得通项公式为$x_n=\sqrt 3[1-\frac{2}{(2-\sqrt 3)^n+1}]$,显然,$\lim_{n\to\infty}\sqrt 3[1-\frac{2}{(2-\sqrt 3)^n+1}]=\sqrt3$,得到答案
方法二:利用数列极限的性质
对于一个一阶递推数列$a_{n+1}=f(a_n)$,如果有$\lim_{n\to\infty}a_{n}=L$
则$\lim_{n\to\infty}f(a_n)=a_{n+1}=f(L)$
而$\lim_{n\to\infty}a_{n+1}=L$
所以$f(L)=L$,也就是说,如果数列有极限,那么极限的值一定是不动点
因此上面的方法中,解出了不动点为$±\sqrt3$的时候,因为$x_1=1$,那么数列恒为正,因此极限一定是大于0的,也就是$\sqrt3$
特征方程
使用条件
二阶线性递推式:$a_{n+2}=pa_{n+1}+qa_n,p,q\in R$
内容
将$a_{n+2}$换成$x^2$,$a_{n+1}$换成$x$,$a_n$换成1,得到方程$x^2=px+q$,这个方程就是递推式的特征方程,其解就是特征根.
- 如果有两个特征根$x_1,x_2$,那么就有$\frac{a_{n+1}-x_1a_n}{a_{n+1}-x_2a_n}$是等比数列
- 如果是两个重根,那么$a_{n+1}-xa_{n}$是等比数列
可以利用此方法将二阶递推数列$a_{n}=f(a_{n-1},a_{n-2})$化为一阶递推数列$a_n=f(a_{n-1})$,达到降阶从而简化问题的目的
原理
$a_{n+2}=pa_{n+1}+qa_n$中左右两边同时减去$xa_{n+1}$得到
$$a_{n+2}-xa_{n+1}=pa_{n+1}+qa_n-xa_{n+1}$$
$$a_{n+2}-xa_{n+1}=(p-x)a_{n+1}+qa_n$$
这里操作的指导思想和前面的不动点类似,也就是如果可以化成
$$a_{n+2}-xa_{n+1}=(p-x)(a_{n+1}-xa_n)$$
的话会有利于研究
于是有关系式
$$1:-x=p-x:q$$
$$q=x^2-px$$
$$x^2-px-q=0$$
说来也怪,这个式子就是刚刚替换掉$a_{n+2},a_{n+1},a_n$的结果,因此我们把这个式子叫做特征方程
接下来对x的个数分类讨论:
首先,由于韦达定理,$x_1+x_2=p$
- $x_1!=x_2$
$$a_{n+2}-x_1a_{n+1}=x_2(a_{n+1}-x_1a_n)$$
$$a_{n+2}-x_2a_{n+1}=x_1(a_{n+1}-x_2a_n)$$
两式相除得到
$$\frac{a_{n+1}-x_1a_{n}}{a_{n+1}-x_2a_{n}}=\frac{x_2}{x_1}\frac{a_n-x_1a_{n-1}}{a_n-x_2a_{n-1}}$$
于是$\frac{a_{n+1}-x_1a_n}{a_{n+1}-x_2a_n}$是等比数列
- $x_1=x_2=x$
$$a_{n+2}-xa_{n+1}=x(a_{n+1}-xa_n)$$
因此$a_{n+1}-xa_{n}$是等比数列
例题
(偷个懒)