复数
复数的概念
引入i满足$i^2=-1$,则$\sqrt{-7}=\sqrt 7 i$
通式:$z=a+bi$,其中a为实部,b为虚部
复数的分类:当b=0的时候,z为实数,b!=0时,z为虚数,当a=0的时候z为纯虚数
两个虚数$a+bi=c+di$相等时,$a=c,b=d$
复数的几何意义
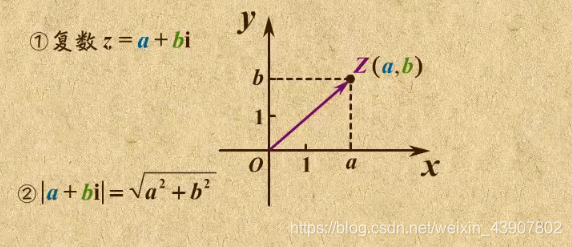
如图的坐标系叫做复平面直角坐标系,y为虚轴,x为实轴
复数$z=a+bi$在复平面坐标中可以用点或向量$(a,b)$表示
复数的模:$z=a+bi$的模为$\sqrt{a^2+b^2}$
圆的复数表示
对于一个复数$z$,式子$|z-(a+bi)|$表示的是复数$z$在复平面上的点到点$(a,b)$的距离(用向量减法即可证明)
如果有$|z-(a+bi)|=c$,那么这个式子即表示以$(a,b)$为圆心,$c$为半径的圆,$z$所代表的点在圆上
复数加减法
实部加实部,虚部加虚部即可
如:$3i+7-2i+3=i+10$
这种计算规则决定了如下关系:两个复数$z_1,z_2$所表示的点为$m_1,m_2$,则$\vec{Om_1}+\vec{Om_2}=z_1+z_2$,因为向量加法是x与x相加,y与y相加,复数加法是实加实,虚加虚,正好等价
复数乘法
直接按照多项式相乘后展开,然后合并同类项(不要忘了$i^2=-1$)
如$(1+2i)(3+4i)(-2+i)=-25i$
共轭复数
实部相等,虚部互为相反数的两个复数是共轭复数
$z=a+bi$,则其共轭复数是$\overline{z}=a-bi$
(其实我们常用的平方差中的两个因式就称作互为共轭式)
共轭复数的性质
$|z|=|\overline{z}|=\sqrt{a^2+b^2}$
$(a+bi)(a-bi)=a^2+b^2$
$z\times \overline{z}=|z|^2=|\overline{z}|^2$
复数除法
使用分母实数化,也就是分数线上下两端同时乘上分母的共轭复数,从而将分母化为常数,转化为加减乘法
$\frac{7+i}{-3+4i}=\frac{(7+i)(4i-3)}{9+16}=\frac{-17}{25}+\frac{-31}{25}i$
复数的乘方中的周期现象
$i=i,i^2=-1,i^3=-i,i^4=1,i^5=i$,因此$i^n$这个数列以4为一个周期.由于这种特殊性质,我们可以借用这种思路来计算一些高次的复数
求:$(\frac{\sqrt 2}{2}+\frac{\sqrt 2}{2}i)^{2015}$
列表如图:

由于$\frac{2015}{8}=251…7$,于是$(\frac{\sqrt 2}{2}+\frac{\sqrt 2}{2}i)^{2015}=\frac{\sqrt 2}{2}-\frac{\sqrt 2}{2}i$
求复数的模
有如下两个规律(暂时不知道如何证明):
- 两个复数的积的模等于两个复数模的积
- 两个复数商的模等于两个复数模的商
然后可以求解一些较为复杂的复数
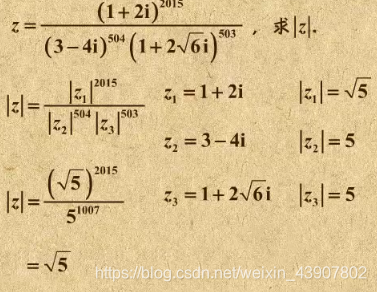
复数与方程
对于一个实系数方程,如果判别式算出来小于0,那么一定有一对互为共轭复数的根,因为根据韦达定理$x_1x_2$为实数
如果对于复系数方程,已知有一个实数根,那么可以假设这个根为b,代入原式中,根据整理后的式子的实部虚部都为0得到这个实数根


