化学常规课基础补救资料
分子的立体构型
思维导图
费曼技巧测试
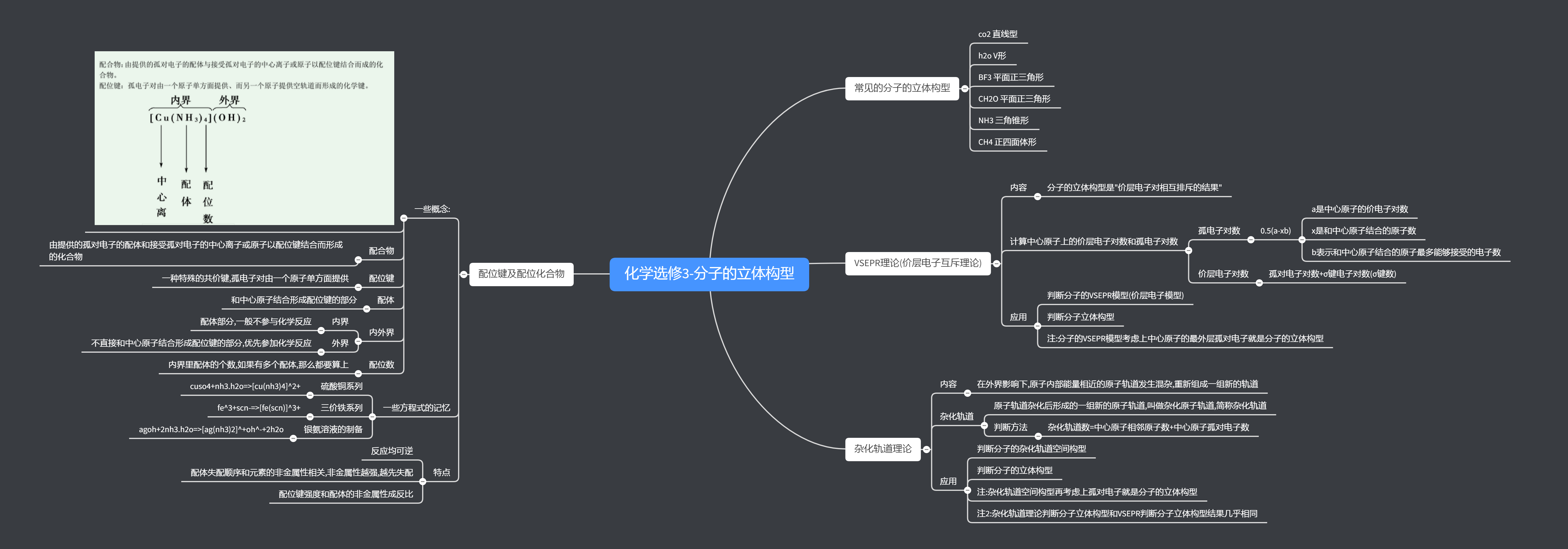
本节讲分子的立体构型,首先是列举了一些常见的立体构型:直线型,$CO_2$,V形,$H_2O$,平面正三角形,$BF_3$,三角锥形,$NH_3$,正四面体形,$CH_4$,$P_4(白磷)$
然后讲了两种分子立体结构的判断理论:VSEPR理论(价层电子互斥理论)和杂化轨道理论
VSEPR理论认为,分子的立体构型由价电子空间构型决定,而价电子空间构型是可以预测的,因此分子的立体构型是可以预测的.具体的预测方法也很简单.本质是把中心原子的价电子空间构型预测出来,然后考虑上中心原子上的孤对电子的影响,从而得到分子的立体构型,如:
- $NH_3$的立体构型的预测:氮元素最外层有5个电子,而一个氢元素最多容纳1个电子,3个氢元素和中心氮元素形成3个$σ$键,因此氮元素最外层上有$3+\frac{5-3}{2}=4$个电子对,而只有3个氢元素,因此有一对孤对电子,而这一对孤对电子对其他的氢原子有排斥作用,因此$NH_3$的分子立体构型是三角锥形
杂化轨道理论是鲍林提出的一种为了解释某些分子的立体构型的理论.其实上面的理论比较完善,但是有一点不严谨:
当分析到$CH_4$这种物质的时候,发现碳元素的核外电子排布式是$1s^22s^22p^2$,最层只有两个孤对电子($2p_x,2p_y$),但是却有4个氢元素和碳元素成了键.众所周知,成键的先要条件是有足够的孤对电子,因此鲍林提出一种理论,认为碳原子的$2s,2p$轨道融合成了4个相同的轨道,每个轨道中一个电子,这样就可以和4个氢元素结合形成4个键参数完全相等的碳氢键,这是我们把那4个新轨道叫做杂化轨道,把这种轨道杂化方式叫做$sp^3$杂化.除开$sp^3$杂化之外,还有$sp^2 \ sp$杂化,s的指数加上p的指数就等于杂化轨道数
杂化轨道理论同样可以预测分子的立体构型,思路和VSEPR非常的相像,即先预测出中心原子的杂化轨道空间构型,然后在考虑上孤对电子的影响从而得到分子的立体构型,for example,$H_2O$,中心原子是氧原子,要计算轨道数,只需要把和中心原子相邻的原子数和中心原子上的孤对电子数相加即可,因为杂化轨道只用来容纳未成对电子和$σ$键,因此水的轨道数$=2+\frac{6-2}{2}=4$,而只有两个氢原子和氧结合,因此还留了两个空轨道容纳孤对电子,因此是V形
最后提到了一个配合物理论,这是我没有怎么搞懂的东西,具体是不知道到底要考什么,我现在学到的东西也就是一些概念和两个方程式($[Cu(NH_4)]^{2+}$,还有个什么也忘了..配合物这部分真的学的糊涂),因此这一部分后面再update.
update 2019年10月13日21:03:26
再次整合了一下配合物的相关知识点,整合到的内容如下:
配合物的定义,即由提供的孤对电子的配体和接受孤对电子的中心离子或原子以配位键结合而形成的化合物,配位键是指一种特殊的共价键,孤电子对由一个原子单方面提供,配体是指和中心离子或原子直接结合,给予中心离子或原子成对电子的分子或离子.配合物的结构分为内界和外界,内界就是配体部分,一般不会参与反应,外界是非配体部分,优先参与反应,还有一个基本概念叫做配位数,即配体的个数,如果有多种配体,应该把他们加在一起得到配位数
经典的配合物的应用有三个:
硫酸铜和氨水反应:$CuSO_4+2NH_3·H_2O=Cu(OH)_2+(NH_4)_2SO_4$,继续滴加氨水得到$Cu(OH)_2+4NH_3·H_2O=[Cu(NH_3)_4]^{2+}+2OH^{-}+4H_2O$
检验三价铁:$Fe^{3+}+SCN^{-}=[Fe(SCN)]^{3+}$
银氨溶液的制备:$AgNO_3+NH_3·H_2O=AgOH+NH_4NO_3$,继续滴加氨水得到$AgOH+2NH_4OH=[Ag(NH_3)_2]^{+}+OH^{-}+2H_2O$
此外,配合物还有一些性质:1.配位键的强弱和配体的非金属性相关,非金属性越强,配位键越弱 2.配体失配的顺序也和配体的非金属性相关,非金属性越强,配体越早失配 3.制备配合物的反应都是可逆反应
关于如何判断分子中是否有配位键,我们从定义入手,找有空轨道的原子和孤对电子的原子,一般来讲是一些经验,多积累?.
end.
以上这些关于配合物的理论还不能够完全解决教材完全解读上面的所有相关题目,真是很可惜啊,没有人能够给我提供帮助,于是我只有到网上去找相关的资源,这耗费了我大量的时间.希望事情会有好转吧
分子的性质
思维导图
费曼技巧测试
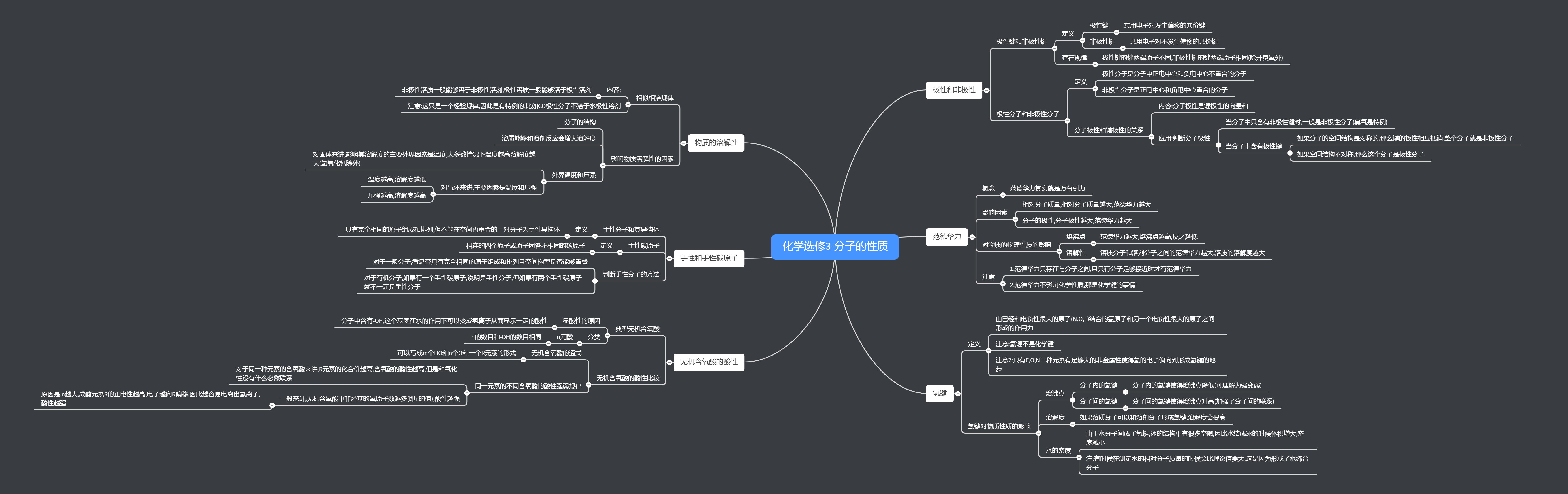
首先是讲极性和非极性.极性共价键和非极性共价键的定义:共用电子对有偏移的是极性共价键,没有偏移的是非极性共价键.一般来讲,判断这两种键的方法就是直接看键两端的原子是否相同,如果相同就说明是非极性共价键,反之是极性共价键.
了解了极性共价键和非极性共价键后,引入一个极性分子和非极性分子的概念.极性分子的定义是正电中心和负点中心不重合的分子,非极性分子的定义是两个中心重合的分子.判断分子极性的方法如下:分子的极性是各个共价键极性的向量和,如果某个分子里的极性向量和为0,那么为非极性分子,如果极性向量和不为0,那么是极性分子.我们还可以从分子的立体构型来判断,如果分子的立体构型是对称的,那么说明分子是非极性分子,反之极性分子;
接下来是讲范德华力,范德华力,说白了就是万有引力,只要距离足够近,分子两两之间都存在范德华力.影响范德华力的因素有分子的相对分子质量和分子的极性.范德华力可以影响物质的熔沸点,具体表现为范德华力越大,分子的熔沸点越高.范德华力还可以影响分子在溶剂中的溶解度,范德华力越大,溶解度越大
之后是氢键,氢键的定义是已经和非金属性很强的原子结合了的氢原子和另一个非金属性很强的原子之间形成的一种相互作用力,可以有趣的理解为由于氢原子的最外层电子有被中心原子抢去的趋势,氢原子和另外一个中心原子达成了使用电子对的口头协议.注意这里的中心原子仅限于$N \ O \ F$元素,因为只有这三种元素才能够让共用电子对偏移到即将被剥夺的地步.氢键也可以影响物质的熔沸点,具体表现是氢键越强,熔沸点越高;当然氢键还可以影响分子在溶剂中的溶解度,如果溶剂和溶质能够形成氢键,那么溶解度增大;氢键还影响了水的密度,因为当水结成冰的时候,由于氢键按照一定的空间构型排列,冰的分子间空隙很大,故密度变小
后面讲了物质的溶解性,首先讲了相似相溶规律(注意这个仅仅是一个规律,不是一个定理,也就是说有例外):极性溶剂易溶于极性溶质,非极性溶剂易溶于非极性溶质.例外是$CO$等.我们可以用这个规律来解释一些溶解的现象
相似相溶过后,探讨了影响物质溶解性的因素:1.分子的结构 2.溶剂和溶质是否可反应 3.固体的溶解度和温度一般成正比($Ca(OH)_2$除外) 4.气体的溶解度一般和温度成反比,和压强成正比
然后引入了手性的概念:一对手性异构体是指一对拥有完全相同的元素种类,个数和排列的但是不能够在空间里重合的分子,有手性异构体的分子叫做手性分子(这个概念之前还打掉了),具体的判断方式就是从定义出发了.接下来讲到一种特殊的手性分子:手性碳原子,定义是四个与其相连的基团都互不相同的碳原子,在有机化学里面,判断一个有机物是否是手性分子,不仅仅可以从定义出发,还可以数手性碳原子的个数:如果有一个手性碳原子,那么就是手性分子,如果有两个就不一定了.
最后是讨论了无机含氧酸的酸性.首先解释了无机含氧酸显酸性的原因:其中含有$OH^{-}$,$OH^{-}$在水的作用下可以电离出$H^{+}$从而显酸性.无机含氧酸可以写成如下通式:$(HO)_mRO_n$,对于同一个成酸元素$R$来讲,其化合价越高,对应酸的酸性越强.而一般来讲,通式中的n越大(其实就是非羟基氧的个数),对应的酸酸性越强,这是因为n越大,R的正电性越大,因此电子就越偏向R,整个酸就越容易电离出氢离子
end.
分子晶体和原子晶体
思维导图
费曼技巧测试
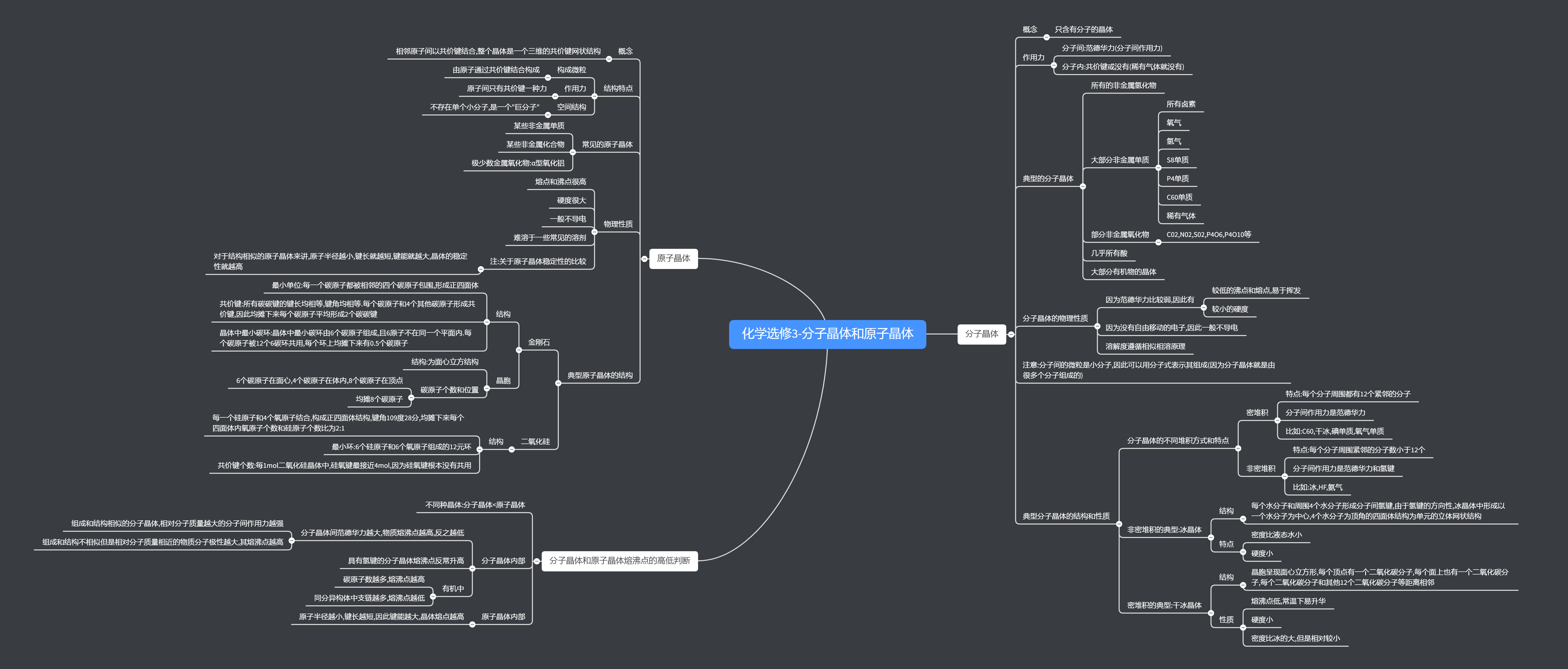
首先是讲了分子晶体.分子晶体是仅由分子构成的晶体,分子间的作用力是范德华力,分子内部的作用力一般是共价键(稀有气体没有).常见的分子晶体一般有:所有的非金属氢化物,大部分非金属单质,部分非金属氧化物,大部分的酸和几乎所有的有机物.由于分子晶体是由范德华力作用的,因此分子晶体熔沸点都不高,容易升华,硬度小,而且基本不能够导电,因为没有自由移动的电子,而且遵循相似相溶原理.
分子晶体的组成方式有两种:密堆积和非密堆积.密堆积是指每个分子都有12个紧邻的分子,这种分子晶体里面一般存在的只有范德华力,另一种非密堆积就是指分子紧邻的分子数少于12个,因此这种分子晶体里面的力除了范德华力之外还有氢键.
典型的非密堆积分子晶体就是冰晶体.冰晶体的结构是由以一个水分子为中心,四个水分子为顶角的正四面体结构为基础而延伸开来构成的空间网状结构,冰晶体的特点就是,由于氢键,密度小于水,且硬度也比较小.典型的密堆积的分子晶体就是干冰晶体.干冰晶体的晶胞呈现面心立方形,每个顶点有一个二氧化碳分子,每个面上也有一个二氧化碳分子,每个二氧化碳分子和其他12个二氧化碳分子等距离相邻.由于干冰晶体是密堆积,因此密度比冰大,但是也很小,而且硬度,熔沸点都不高
然后引入原子晶体,原子晶体是指由原子构成的,共价键作用的晶体,微粒子间的作用很显然是共价键,常见的原子晶体一般有:一部分非金属单质和一些非金属化合物(说了和没说一样啊),还有一个特例是一个金属氧化物:$α$形氧化铝.共价键一般很强,因此原子晶体一般硬度大,熔沸点高达上千摄氏度,且不溶于常见溶剂(具体溶于什么我也不晓得)
常见的原子晶体有两种:金刚石和二氧化硅
金刚石中,每一个碳原子和其他四个碳原子成键,是$sp^3$杂化,4个碳原子成正4面体形,金刚石按照这种基本形式展开成为一个网状结构(也就是很多地方说的巨分子),金刚石中,一个$C-C$键分别属于两个正四面体结构,而一个碳原子分别和其他4个碳原子成键,因此一个碳均摊下来形成2根$C-C$键
(思考:这里提到了均摊法,而之前的均摊法是用在晶胞中的均摊法,这里的均摊法是用在正四面体结构上的,但是并没有详尽关于均摊法使用对象,也就是基本单位(晶胞,正四面体,或是其他什么乱七八糟的东西)的定义,所有应该怎样去理解这个现象,难道是因为无论怎样定义这个基本单位,计算出来的分子式都是一样的吗?诶好像有理解这个问题的思路了,也就是说,基本单位的定义就是:整个晶体是这个基本单位按照一定规律重复得到的结构,只要满足这个定义,基本单位怎么定义都是可以的,这样理解不知道对不对)
金刚石中还有一种基本单位叫做6碳环,也就是6个碳组成的一个环,这6个碳中的每一个又被其他的12个6碳环共用,因此一个6碳环均摊下来相当于是只有$6\times \frac{1}{12}=\frac{1}{2}$个碳原子
介绍完金刚石的结构后我们介绍一下金刚石的晶胞:金刚石的晶胞是面心正六边形结构,有6个碳原子在面心,8个碳原子在顶点,4个在体内,均摊下来有8个碳原子
除开金刚石外,还有一种原子晶体叫做二氧化硅,每一个硅原子和4个氧原子结合,构成正四面体结构,键角109度28分,均摊下来每个四面体内氧原子个数和硅原子个数比为2:1,因此二氧化硅才叫$二$氧化$(一)$硅..
二氧化硅也有类似于金刚石的最小环结构,但和金刚石不同的是,二氧化硅的最小环结构是有12个原子的,6个$Si$6个$O$;二氧化硅中每个$Si-C$键不发生共用,而一个$Si$元素一般会和4个氧元素成键,因此在$n \ mol \ SiO_2$晶体中一般含有$4n \ mol \ Si-C$键
(说实话我感觉这一节的主要知识记忆的不牢固,这次费曼技巧都进行的非常卡顿)
接下来是一些关于晶体硬度和熔沸点判断的技巧性知识
首先来讲硬度,对于结构相似的原子晶体来讲,其原子半径越小,共价键就越稳定,硬度相应越大
接下来是熔沸点.如果比较分子晶体和原子晶体的熔沸点的话,显然分子晶体要低得多.如果比较两种分子晶体的熔沸点大小的话,考虑分析分子间的范德华力:对于结构相似的分子,相对分子质量大的熔沸点高,因为范德华力大;对于结构不相似但是相对分子质量相近的,分子极性越大,熔沸点越高,原因同理.如果这两个不能分析,那么考虑如果分子间有氢键,那么熔沸点反常升高;在有机化学里面,碳的个数越多,熔沸点高,在同分异构体中,支链越少,熔沸点越高.如果比较原子晶体的话,还是比较原子的半径大小,和硬度相似
end
#共价键
(DMR 2019.10.11)
思维导图
费曼技巧测试
上午看了共价键一节
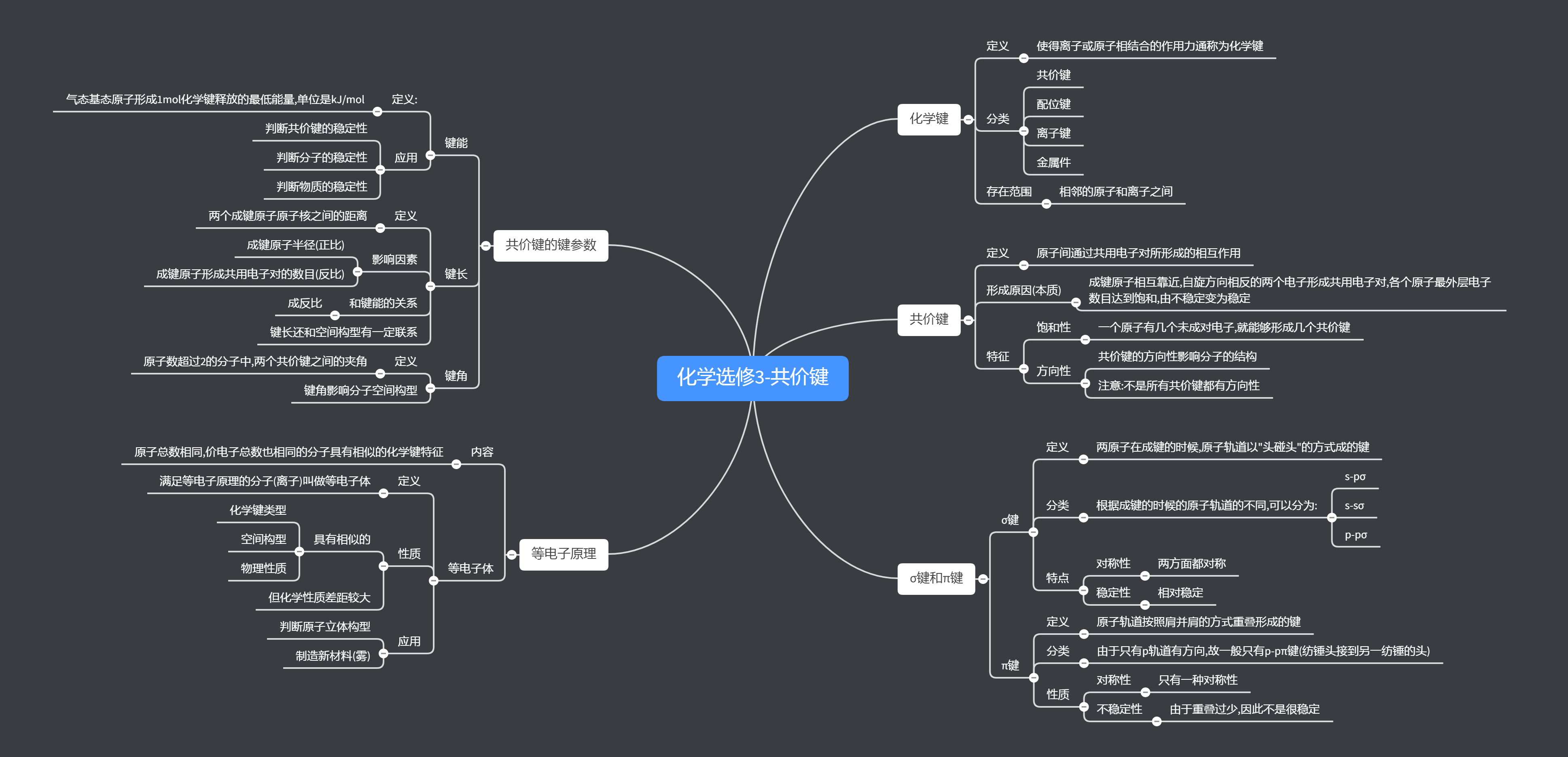
这一节主要讲了化学键中的共价键,既然这样,那就先讲一下化学键是什么东西.化学键就是原子之间相互结合而产生的作用力,化学键一般分两种:离子键和共价键(还有一个配位键我现在还没有学到),离子键比共价键稳定,判断两个元素成键的类型可以用电负性差值的大小来判断,当然也可以粗糙的用成键元素的金属和非金属性来判断,只是要记住一个特例,$AlCl_3$
化学键中的离子键不是今天研究的重点,今天的重点是共价键,共价键的定义是:成键原子之间共用电子对而形成的作用力,共价键有两个特性:方向性和饱和性,方向性是指有一些共价键是有方向的,饱和性是指每个原子的成键总数或以单键相连的原子数目是一定的
接下来是讲共价键的分类了.我们根据共价键成键轨道和形式的不同将共价键分成两种:$σ键$和$π键$:
$σ键$是轨道头碰头形成的共价键,而$π键$是轨道肩并肩形成的共价键,$σ键$,按照成键的轨道不同,也可以详细的分为$s-s \ σ键$,$s-p \ σ键$,$p-p \ σ键$,$π键$一般只见到$p-p \ π键$,由于$σ键$是头碰头形成的,电子云重叠的比较多,因此比较稳定,相对应的$π键$就比较不稳定了,而根据共价键的方向性,两个原子间能且只能形成一个$σ键$,其他的都是形成的$π键$,且$σ键$首先形成,还值得一提的是,这两种键都是有对称性的,区别在于$σ键$有轴对称和镜面对称,$π键$只有镜面对称
共价键的分类之后是共价键的参数:键长,键能,键角
键长是指成键原子原子核之间的距离,受成键原子核电荷数和共用电子对个数影响,且一般来讲,键长越长,共价键越不稳定,越容易断,且和分子的空间构型有一定关系
键能就是气态基态原子形成1mol化学键释放的最低能量,单位是kJ/mol,键能受键长的影响,键能和很多东西都有关,一般常见的是:键能越大,共价键越稳定,化合物越稳定,越不活泼
键角一般只考虑它和分子空间构型的关系
以上是本章的主要内容,还有一个等电子体简单提一下:
- 等电子原理,指原子个数相等且核外电子也相等的分子具有相同的化学键性质和物理性质,但化学性质不保证相似
- 等电子体,即满足等电子原理的分子,这些分子之间有相似的性质
这个东西有什么用呢?首先是用来判断分子的立体构型,即等电子体的分子具有相似的立体构型,其次是制造新材料,利用他们相似的物理性质,这第二点作为了解就好吧
金属晶体
思维导图
费曼技巧测试
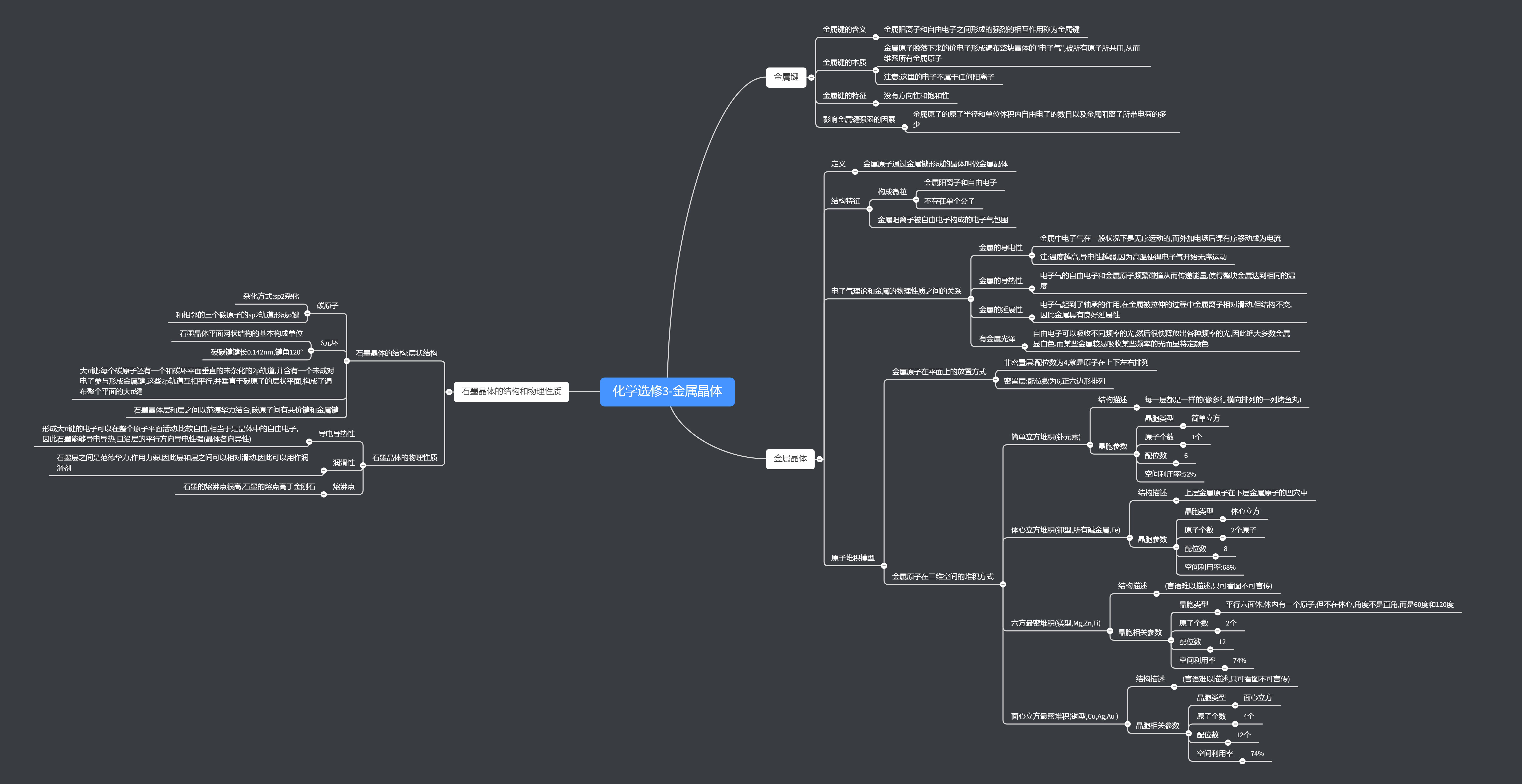
首先引入金属键的概念:金属键就是指金属阳离子和电子的强烈相互作用.本质是电子气和金属离子之间的相互作用.电子气:金属晶体中的所有金属阳离子失去电子,从而晶体中的电子为所有的金属原子所有.就像包围着地球的气体属于大家所有人一样,这种电子气体与金属原子之间形成了非常强烈的相互作用,这种相互作用叫做金属键.
电子气和金属的大部分性质都是相关联的:金属的导电性是因为电子气和中的电子可以自由移动的缘故,导热性是因为电子气中的电子可以快速的和金属原子碰撞从而传递能量使得整块金属快速的升温到同一温度,有金属光泽是因为电子气可以吸收所有颜色的光,然后快速的放出各种颜色的光,所以一般的金属都显银色.有些金属显特殊的颜色是因为其电子气更偏向于吸收某种颜色的光.而金属有延展性是因为电子气在金属原子中间起到了轴承的作用,因此金属原子在外力挤压下虽然会发生相对移动,但是结构是不会变的,因此具有很好的延展性
金属键没有方向性和饱和性,且其强弱和原子的半径,单位空间自由电子数,金属阳离子所带电荷数有关
接下来是金属晶体的概念:金属原子间通过金属键的作用形成的晶体叫做金属晶体.金属晶体中的微粒只有自由电子和金属原子,作用力是金属键
金属晶体在平面上的堆积方式有两种:密置层和非密置层.密置层就是一个原子周围有6个其他的原子,非密置层就是原子上下左右有其他原子,因此这两种方法的配位数分别是6和4
金属晶体在三维空间上的堆积方式有4种.
第一种是简单立方堆积.这种堆积就是很简单的非密置层重叠,很显然可以从其立体结构中提出一个正立方体晶胞,因此这种堆积方式名字叫做简单立方堆积,其空间利用率为52%(计算过程稍后给出),配位数(这里的配位数是指距离一个原子最近的原子个数)为6,均摊下来每个晶胞中有1个原子,一般常见的有钋$Po$元素的晶体按照这种方式堆积
第二种是体心立方堆积.这种堆积的结构是非密置层交错重叠,可以从中划分出一个体心立方晶胞,因此得名体心立方堆积.空间利用率为68%,配位数为8,均摊下来每个晶胞2个原子,由于所有的碱金属都是这种堆积方式,因此也叫做钾形堆积,除开非金属外,还有$Fe$元素的晶体也按照这种方式堆积
第三种是六方最密堆积.这种堆积结构难以一言蔽之,自己看图去.画图可得,其中可以划分出一个平行六面体晶胞(注意不是正六面体,夹角是60°和120°),画图可得,这个晶胞的空间利用率为74%,利用率最高,配位数为12,均摊下来每个晶胞中有2个原子,常见的有$Mg \ Zn \ Ti$,因此也叫镁型
第四种是面心立方最密堆积,结构同样难于一言蔽之,其中可以画出面心立方晶胞,因此得名.这个晶胞的空间利用率和六方最密堆积一样,为74%,因为这两种堆积方式在堆积很多层后基本上没有什么太大的差别(边界除外.在一大块晶体中,中心的结构六方和面心差不多,但是边界上就不一样了,这就是他们两个的晶胞形式不一样的原因),配位数也是12,均摊下来每个晶胞中有4个原子,常见的有$Cu \ Ag \ Au$(都不便宜啊),因此也叫铜型(个人认为应该叫贵型~~)
后面讲了石墨晶体的一些特点.
首先是石墨晶体的结构.石墨晶体中碳原子是$sp^2$杂化,和相邻的3个碳原子形成$σ$键.石墨晶体中的基本结构是6碳环,这种6碳环中均摊下来仅有3根$C-C$键,2个碳原子.碳原子是可以形成4根键的,而一个碳原子只和其他三个碳原子形成了键,因此一对孤对电子在垂直于原子平面的方向参与形成了$π$键,因此石墨晶体中有遍布整个原子平面的大$π$键,因此石墨的碳原子层和层之间是有类似于自由电子的东西的.因此,石墨晶体层和层之间是由范德华力维护,同层之间的碳原子之间有共价键和金属键(这里有点不符合逻辑啊,为什么碳原子之间还有金属键啊)
接下来是石墨晶体的一些性质.石墨晶体的导电和导热性是由于形成大$π$键的电子是可以在层间自由移动的,石墨晶体的润滑性也是因为其层状结构.最后一个性质就是石墨晶体的熔沸点很高,其熔点高于金刚石
接下来是补充堆积方式的空间利用率的计算:
设晶胞中原子体积为$V_{a}$,晶胞体积为$V_{b}$,空间利用率为$X$
- 立方堆积:
$V_{a}=1\times \frac{4}{3}π r^3=\frac{4}{3}πr^3$
$V_{b}=(2r)^3=8r^3$
$得到X=\frac{V_{a}}{V_{b}}=\frac{π}{6}=0.52333333333333333333333333333333…….$
- 体心立方堆积:
$V_{a}=2\times \frac{4}{3}π r^3=\frac{8}{3}πr^3$
根据立方体对角线等于4倍原子半径得到:
$V_{b}=(\frac{4 \sqrt{2}r}{3})^3=\frac{64 \sqrt{3}}{9}r^3$
$得到X=\frac{V_{a}}{V_{b}}=\frac{\sqrt{3}π}{8}=0.67982994197078433770952268904105…….$
- 六方最密堆积
$V_{a}=4\times \frac{4}{3}π r^3=\frac{16}{3}πr^3$
设$S$为底面菱形的面积,则$S=2r\times (2r\times sin60°)=2\sqrt3r^2$
设$H$为平行六面体的高度,根据平行六面体内部原子所处高度为整个六面体高度的一半且和其他的4个底面原子形成正四面体这个条件得到
$H=2\times(\sqrt{(2r)^2-(\frac{2\sqrt3}{3}r)^2})=\frac{4\sqrt6r}{3}$
$V_{b}=S\times H=\frac{4\sqrt6r}{3}\times 2\sqrt3r^2=8\sqrt2r^3$
$得到X=\frac{V_{a}}{V_{b}}=\frac{\frac{π}{3}}{\sqrt2}=0.74010509764191974220621709900308……..$
- 面心立方最密堆积
$V_{a}=4\times \frac{4}{3}π r^3=\frac{16}{3}πr^3$
$V_{b}=(2\sqrt2r)^3=16\sqrt2r^3$
$得到X=\frac{V_{a}}{V_{b}}=\frac{\sqrt2π}{6}=0.74010509764191974220621709900308…….$
end
晶体常识
思维导图
费曼技巧测试
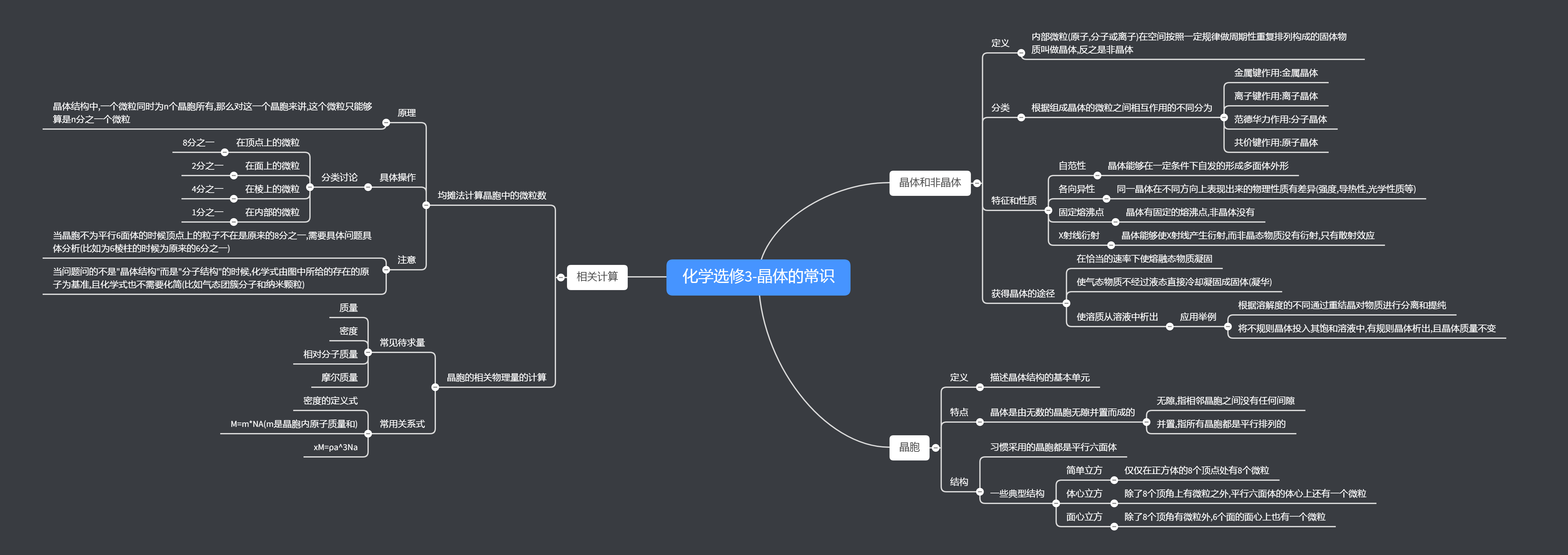
晶体的常识一节首先引入了晶体的概念:内部微粒(原子,分子,离子)按照某种规律重复排列所构成的固体叫做晶体.且我们根据晶体内部作用力的不同把晶体分为:金属键作用的金属晶体,离子键作用的离子晶体,范德华力作用的分子晶体和共价键作用的原子晶体.
晶体有一些特殊的性质:1.自范性,即晶体在某些环境下会自动形成具有规则的几何结构的固体. 2.各向异性,即晶体在不同方向显示出来的物理性质(导电性,导热性,光学特性等)不同 3.晶体都有固定的熔沸点 4.晶体可以使得X射线发生衍射(当然具体我也不知道这是个什么鬼东西)
获得晶体的方法大概有三种:你可以让气态物体直接凝华,也就是让某种气体不经过液态直接凝固成固态,从而得到晶体.你还可以让熔融态物质在恰当的速率下冷却从而得到晶体.还有一种方法是让晶体从溶液中析出,比如你把残缺的$NaCl$晶体放到饱和氯化钠溶液中就可以得到完整的$NaCl$晶体
为了方便研究晶体的性质,我们引入了一个晶胞的概念.晶胞,就是晶体中的最小单位,整个晶体就是由晶胞重复堆叠而成的.晶胞的结构一般为平行正六面体(不一定是长方体!),典型的晶胞结构可以分为3种:仅在4个顶点有原子的叫做简单立方,在简单立方的基础上体心上还有一个原子的叫做体心立方,在简单立方的基础上在6个面的面心上还有原子的叫做面心立方.但在做题的时候会遇到更加恶心的东西
之后就是本章的计算版块,我们需要用均摊法研究晶体的微粒数,并在此基础上研究晶体的相关物理量:密度,体积,相对分子质量,以至于阿伏伽德罗常数等.
均摊法就是一个公式:$X=kx$,大写的X是某一个微粒在晶胞中实际占有的个数,小写的x是指由多少个位置相似的微粒,k就是比例常数,代表着此位置上的微粒实际上由几个晶胞共有.假如某晶体的晶胞长成正6棱柱,那么这个晶胞中的顶点上的一个微粒就会被12个晶胞共用,因此$X=1\times\frac{1}{12}=\frac{1}{12}$,也就是说,实际上一个晶胞中仅拥有十二分之一个此微粒.
关于相关的物理量的计算,一般来讲就按照自己的思路走就可以,但是一般的资料书上会把常问的物理量组合起来写成一个关系式:$a^3ρN_A=xM$,a的立方是晶胞的体积(有时候并不是正方体,因此不能够直接带入a的立方),$ρ$是密度,$N_A$阿伏伽德罗常数,x是一个晶胞中含有的基本粒子的个数,M是基本粒子的相对分子质量,因此就可以根据1摩尔晶胞的质量相等这个等量关系来列出这个式子了,不得不说这是一个快速计算的好方法,听寝室里的同学讲理综的时间非常不够,需要读一遍题就出答案,这个时候也许套公式比自己算要更快一些.当然,套公式和自己算两种方法最后得出的结果理论上来讲是等价的
离子晶体
思维导图
很可惜的是,我的幕布会员过期了,这也就意味着我不能够导出.png形式的思维导图,看来应该支持一下开发者了,就充一个月~~9元不算很贵的啊
费曼技巧测试
首先引入离子键这一概念
离子键是由于阴阳离子之间的静电作用而形成的一种化学键.要形成离子键,首先要一方原子有很强的得电子能力,另外一方原子有很强的失电子能力.一般来讲,两方原子电负性差值大于1.7就可以认为可以形成离子键.当然有两个特例:$NaH \ KH$,这两个离子晶体内部元素的电负性差的绝对值小于1.7.离子键没有方向性和饱和性,原因很简单,如果空间允许,一块磁铁可以365度无死角的吸引世界上的所有金属.离子键这个概念的意义和前面的金属键等一样,在于衡量离子化合物的稳定性.离子键的强弱和离子的带电数和离子的半径有关,这一点在后面讲晶格能的时候会提到
接下来是讲离子晶体
离子晶体就是阴阳离子之间以离子键为相互作用力而形成的晶体.显然,离子化合物之间的作用力是离子键,并且构成其的微粒是阴阳离子.在堆积方式上,由于离子键没有方向性和饱和性,可以把离子晶体看做是不等径圆球的密堆积.
典型的离子晶体有:$NaCl \ CsCl \ CaF_2$,接下来一一介绍.
因为氯化钠的晶胞是面心立方+体心,因此$NaCl$中钠离子和氯离子的配位数都是6,而一个钠离子周围和其等距离的钠离子个数为12个.由于钠离子和氯离子在空间中是等效的,因此氯离子周围的等距氯离子也是12个.根据均摊法,一个晶胞中含有4个钠离子,4个氯离子
$CsCl$的晶胞是体心立方,你可以理解为体心一个$Cl$,面心一个$Cs$,也可以反过来理解,因为在空间中两种离子位置等效.因此两种离子的配位数为8,而一种离子周围和其等距离的同种离子个数为6,均摊下来每个晶胞中1个$Cs$1个$Cl$
$CaF_2$的晶胞比较神奇,是一个面心立方内部加上8个氟离子,百度百科把这个叫做萤石型结构(不禁想起$Minecraft$里的萤石).大概长这样:
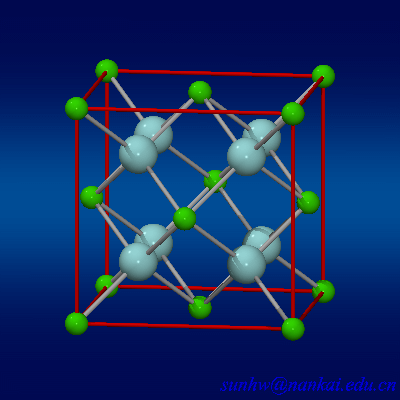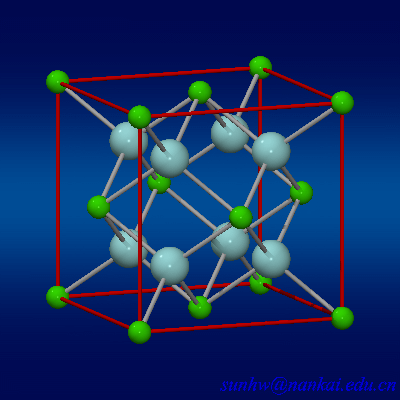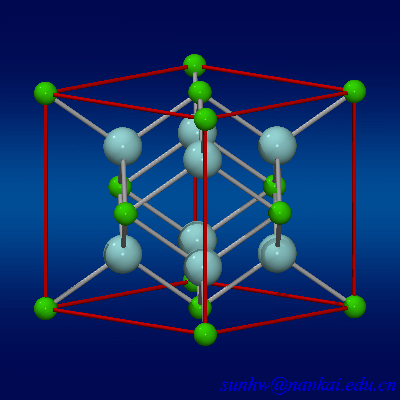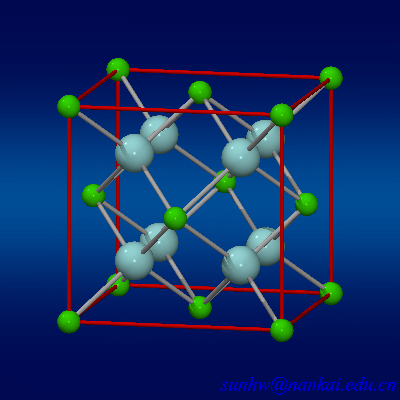
反正一个钙离子的配位数为8,氟离子的配位数为4(这个比例从化学式中也能够看得出来),阴离子$F^-$填充在四面体空隙中,面心立方点阵对角线的$\frac{1}{4}$和$\frac{3}{4}$处,因此$CaF_2$中的最近的钙离子和氟离子之间的距离为$\frac{1}{4}$体对角线长度
最后引入了晶格能的概念.晶格能的定义是气态离子形成1mol离子晶体释放是能量,单位为千焦每摩尔($kJ$/$mol$),影响晶格能的大小的因素可以用库仑定律来理解:$F=k\frac{Q_1Q_2}{r^2}$,晶格能的大小也就和成键离子的带电荷数的乘积成正比,和其间距离的平方成反比(可以直接理解为和距离成反相关就行,反正不需要定量研究).晶格能影响晶体的物理性质,也就是熔点和硬度.可以用一句话讲清楚他们之间的关系:晶格能越大,离子键越稳定,因此晶体越稳定,表现为硬度越高,熔点越高.
元素周期律
(from DMR 2019.10.10)
思维导图
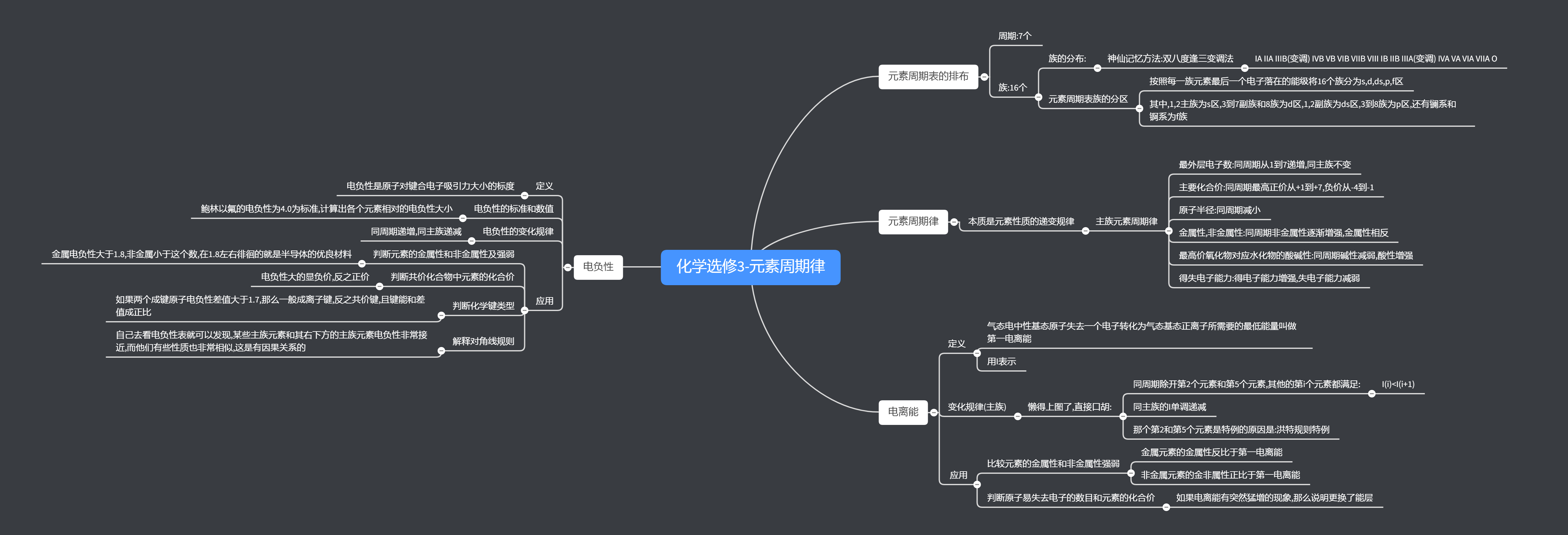
费曼技巧测试
今天的章节是元素周期律
首先要探讨元素周期表
元素周期表有7个周期,16个族,18个纵行,这些族分别是$IA \ IIA \ IIIB \ VIB \ VB \ VIB \ VIIB \ VIII \ IB \ IIB \ IIIA \ IVA \ VA \ VIA \ VIIA \ O$
然后继续对族进行分类,即按照每一主族的最外层电子最后落在的能级分类:
IA,IIA,s区
IIIB,VIB,VB,VIB,VIIB,VIII,d区
IB,IIB,ds区
IIIA,IVA,VA,VIA,VIIA,O,p区
这样一来就可以根据元素的价电子排布式来判断元素在元素周期表中的位置了:
价电子排布:
$ns^{1,2}$,第n周期第1或2主族
$(n-1)d^{i}ns^{j},i+j<=7$:第n周期第$i+j$副族
$(n-1)d^{i}ns^{j},i+j \in [8,10]$:第n周期第VIII族
$(n-1)d^{10}ns^{1,2}$:第n周期第1或2副族
$ns^2np^{1,2,3,4,5,6}$:第n周期第1,2,3,4,5主族或O族
(据说这个O族本来不是零的意思,它是印度语里轮回的意思)
接下来要研究的就是元素周期律了
元素周期律中主要研究这些问题:
原子半径
元素金属/非金属性
元素最高价氧化物的水化物的酸碱性
元素得失电子能力
上面这些问题在必修阶段(也就是高一的时候)已经详细的研究过了,当然,还不完整,但是基本上足够,一般就按照必修阶段的理论判断
为了完善这个体系,我们引入两个概念:第一电离能和电负性
第一电离能:气态基态原子…(诶我记不到这话怎么背的了,抄一段:)气态电中性基态原子失去一个电子转化为气态基态正离子所需要的最低能量叫做第一电离能,这个东西其实就是衡量原子失去电子能力的一个指标
(但是有一个问题啊,第一电离能的使用条件是气态基态原子,但是为什么其他的原子也在使用这个指标呢?其他的原子都成了气态???)
暂且不管这个问题,继续
关于第一电离能的递变趋势有一张表(看来必须要把图片搞上来了)
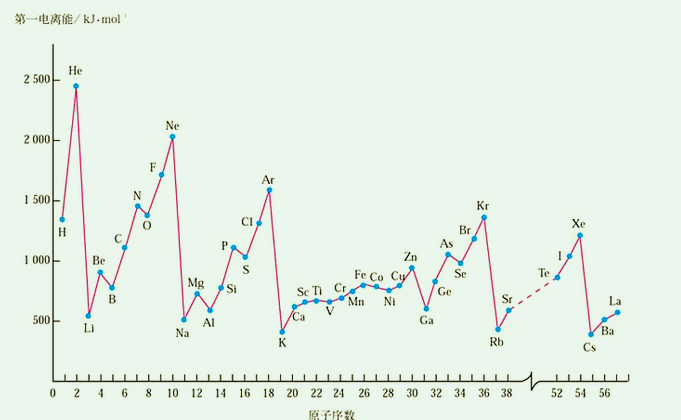
这张表是需要记忆的,但是记忆也很简单的,大概只需要记住以下两条规律:
同周期(特指短周期)从左往右第一电离能除第2,5个外单调递增
同主族从上往下第一电离能单调递减
为什么每一周期第2,5个是例外呢?这是因为洪特规则的特例:每一周期的第2个的价电子排布式是$ns^2$,第3个是$ns^2np^1$,按照洪特规则的特例,$ns^2$比$ns^2np^1$稳定,因此失去一个s上的电子比失去一个p上的电子更耗能量.同理,第5个的价电子排布式是$ns^2np^3$,第6个是$ns^2np^4$,显然,洪特规则告诉我们,半满的相对稳定,因此失去一个半满的p上的电子比失去一个非半满的p电子更耗能量
掌握了这张表,电离能基本上就ok
接下来是电负性,它的定义就是:原子对键合电子吸引力大小的标度,本质上就是衡量原子吸引电子能力的大小的一个指标,关于它的大小关系,也有一张表,是鲍林以F元素的电负性为4.0为基准算出来的每一个元素的电负性表,这个表不需要背到数值,只需要记住如下规律即可:
电负性同周期单调递增,同主族单调递减
两个元素形成化合物的时候,电负性大的显负价,小的显正价
如果两个元素电负性差的绝对值大于1.7,那么他们形成的化合物的化学键一般是离子键,反之是共价键
利用电负性可以判断元素的金属性和非金属性,分解线是1.8
原子结构
(from DMR 2019.10.9)
思维导图
费曼技巧测试
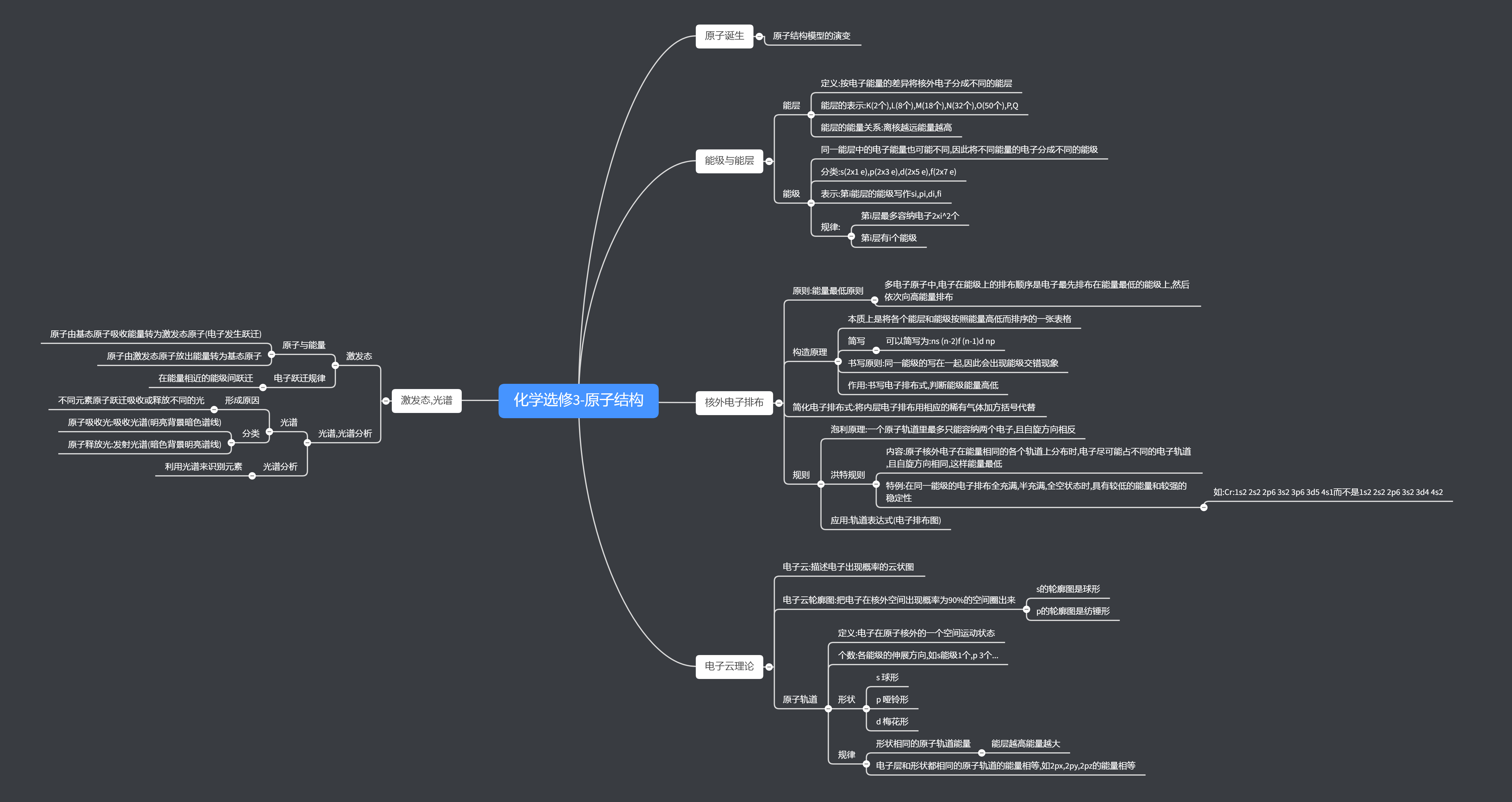
第一章第一节,原子结构,主要是要讲清楚原子核外电子的构成
首先讲能级和能层
为了区分不同位置电子的能量大小,我们引入一个能层的概念,即把原来的核外电子分为7个能层,分别是K,L,M,N,O,P,Q,可以简单记为从国王到皇后~~
每一个能层其实就是一层核外电子,这个就相当于我们初中学的那个核外电子排布规律了
但是注意到每一个能层里面的电子能量还是有很大的差异性,因此我们继续详细探究,把同一个能层分为几个能级
具体怎么分呢?
首先,第i层能层就有i个能级
然后,一共来讲有6种能级,高中阶段值只讲四种:s p d f
对于第i层,就有is ip id if能级(但数量要保证合法)
那么每一个能层就可以分出能级来了:
K:1s
L:2s2p
M:3s3p3d
N:4s4p4d4f
…
但分出了能级有什么用呢?
在讲用处之前,我们讲一个原子轨道理论
原子轨道,就是电子在原子核外的一个空间运动状态,而上面我们讲到的每一个能级的一个伸展方向就是一个原子轨道
原子轨道可以容纳电子,具体来讲,1个s可以容纳2个电子,1个p可以容纳6个电子,1个d可以容纳10个电子,1个f可以容纳14个电子,
那么这个时候,我们只要知道每一个能层有多少个什么能级,就可以知道每一个能层能够放多少个电子了
但是核外电子难道就直接按照能层从低到高依次排列嘛???no!
首先,核外电子的排列需要遵循一个原则:能量最低原则,即先填充能量较低的能层和能级
而有些能级和能层的能量大小关系不是非常的明确的,比如说吧:3d和4s能级的能量就不是一般想的那样:3d<4s,而是3d>4s,这是科学研究证明过的
那么到底是怎样排列的呢????这里,为了方便知识储备不够的高中生学习,各位化学教授大佬们编写了一张表,取名为构造原理:
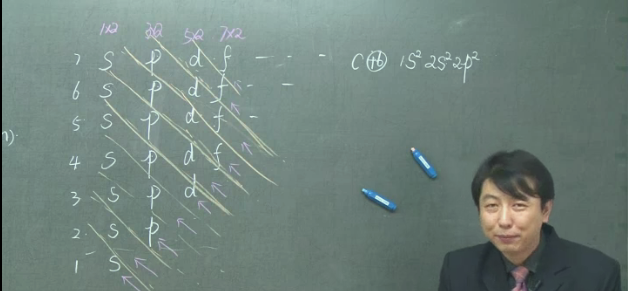
这张表是什么意思呢?看到那条对角线了吗?我们填充的顺序就是按着那条对角线斜着向上,到头了就返到下一层的对角线开始的地方继续走
这就是构造原理了
比如说吧:Fe元素,第26号元素,填充出来的电子排布式就是:$1s^2 \ 2s^2 \ 2p^6 \ 3s^2 \ 3p^6 \ 3d^6 \ 4s^2$
那么如果我要画出电子排布图怎么办?比如一个p能级里面有4个电子,这4个电子又是怎么排的呢???
这就要引入两个个大佬提出的原理了:泡利原理和洪特规则
泡利原理:一个原子轨道里最多只能容纳两个电子,且自旋方向相反
洪特规则:原子核外电子在能量相同的各个轨道上分布时,电子尽可能占不同的电子轨道,且自旋方向相同,这样能量最低
那么按照这两个规则,一个p能级里面有4个电子,就相当于是3个原子轨道中有一个是被占满了的,另外两个只有一个电子
但是,事情还没完,洪特先生发现一些特例不满足他提出的规律:
当某一能级的电子数为半满,全满或全空的时候,能级能量较低且趋于稳定
比如铜元素的电子排布式就应该这样写:$1s^2 \ 2s^2 \ 2s^6 \ 3s^2 \ 3s^6 \ 3p^6 \ 3d^{10} \ 4s^1$,而不是$1s^2 \ 2s^2 \ 2s^6 \ 3s^2 \ 3s^6 \ 3p^6 \ 3d^{9} \ 4s^2$
以上就是本章节最最重要的知识了,感觉还掌握的可以,只是原子轨道和泡利原理和洪特规则掌握的稍显不熟悉
剩下一点点就是:电子云理论,激发态和光谱,这些比较简单,就不测试了


