CTF初探_密码学笔记
C1:导论
密码学分为以下几个分支:
密码学(密码编码学)包含:
- 密码分析学
- 密码使用学
可以大概理解一下:
密码分析学是指破解密码的技巧
密码使用学是指制造密码并且用密码进行交流
两者是互逆的
其中密码使用学可以分为:
- 对称算法:用同一个密匙加密解密
- 非对称算法:利用公匙进行加密
- 密码协议
- 哈希函数
一般加密的时候都是混在一起加密,取长补短
对于一个加密体系来说,一般加密和解密算法都会公开,这样才能够说明这个体系经得起检验.如果仅仅是通过保密加密方式来加密的话,一旦加密方式被破解,就…就完辽
所以,一般来讲,安全传输信息的关键是安全的传递关键数据,比如现在就是安全的传递密匙
简单对称加密:替换密码
密码使用
思路很简单,用一个字母替代另外一个字母,这样文本就乱掉了
密码分析(破解)
方法一 蛮力破解
很简单,这里的关键信息不就是替换的规则嘛,那就暴力枚举所有可能的替换的规则.如果说能够得到一些些原文和密文的片段,然后就可以这样暴力破解了.
假设是英文,那就是26个字母相互替换,就可能有$26!$种可能性,一个个尝试嘛,反正是尝试的出来的,只是时间……长了一丢丢(万一运气好勒,第一个就遇到了不是很舒服)
方法二 频率统计
但凡英语句子都有一些规律,比如哪些字母出现的频率多哪些频率少,比如哪些单词频繁出现,比如哪些字母后面很可能跟上哪些字母等等
替换密码并没有避开这些规律,所以可以利用这些规律来进行破解.这更加的高效.
密码分析概述
密码分析的几种方式
密码分析有如下几种方式:
- 古典密码分析
- 社会工程
- 实施攻击
古典密码分析就是指从密文恢复为明文,包括数学分析法和蛮力法
社会工程就是通过人际交往等方式来获得密码和关键数据,包括欺骗,绑架勒索,冒名,侦探等方式.
实施攻击,从书上的意思大概就是说对处理密码的设备进行探测从而分析出密码什么的
可靠的加密方式是什么样子的
Kerckhoffs原则:密码系统应该就算被所有人知道系统的运作步骤,仍然是安全的。
多长的密匙才相对安全
一般来说,56-64位几个小时(几天),112-128一般计算机要几十年,256就比较困难,量子计算机也需要几十年吧
不过摩尔定律告诉我们,这个数据不会保持太久
模运算以及多种古典密码
模运算
定义
老相识了:
其一:
假设有$a=b\times c+r$,也就是$a\div b=c\dots r$,或者写成$a-r=b\times c$
那么就可以这样写:$a\equiv r\pmod{b}$,也就是说a和r在b下同余,也可以理解为r为a除以b的余数
其二:
求a除以b得到的余数为r,可以表示为$a\bmod b =r$,这里r肯定是在0到b之间的
这第二种方法也可以转化为第一种:
$a\bmod b=r$等价于$a\equiv r\pmod b$
但本质都一样,都是a除以b得到的余数为r
等价类
发现一个问题:对于同余操作$a\bmod b=r$来说,如果不断增大a,那么r的值会有规律的从0增大到b-1然后再回到0,也就是说,某些不同的数字代入到a中获得的结果是一样的.
比如$a\bmod 4=b$,$a=1,5,9,13,17…$的时候b都等于1
同时我们还发现,这些数之间的差都是4,也就是除数.
因此我们把这些不同的a组成的集合叫做一个等价类,每个等价类里面相邻两个数的差值都是除数.
在计算固定模数的操作中,这个东西可以带给我们计算上的便利.(都1202年了,就离谱)
整数环
这个东西是这么构成的:
- 集合Z={0,1,2,3,4,….,m-1}
- 两种操作方式:
$a+b\equiv c\pmod m,c\in Z$
$a\times b\equiv c\pmod m,c\in Z$
它有一些性质:
- 加法
加法逆元存在,也就是说存在$a+(-a)\equiv 0\pmod m$,只是-a不在环里面而已
- 乘法
乘法逆元不一定存在,也即不一定存在$a\times b\equiv 1\pmod m$,其中b为a的乘法逆元
寻找乘法逆元可以使用欧几里得算法(只是我已经不会了),但如果要判断,则可以使用比较简单的方法:如果$gcd(a,m)=1$,则此时存在$a\times b\equiv 1\pmod m$
如何证明呢?原来写过关于裴蜀定理的博客,有点搞忘了,贴过来一下:
裴蜀定理
内容
若$d=(a,b)$(注意这里($a,b$)是指a和b的最小公因数的意思)
则$\exists m,n$使得 $a\times m+b\times n=d$
证明
考虑用数学归纳法证明:
当$b=0时:$
$显然a=d,a可以取任意值,存在m,n满足上式$
$当b>0时:$
$假设对于x\in [0,b-1],都满足上式,其中a可以取任意值$
$首先,显然(a,b)=(b,a\pmod b)=d$
$则对于c=a\pmod b,由于c\in[0,b-1]$
$故:b\times m+c\times n=d ——(\theta)$
$由带余除法得:a=k\times b+c,即c=a-k\times b$
$将c代入(\theta)中得b\times m+(a-k\times b)\times n=d$
$整理得a\times n+b\times(m-k\times n)=d$
$则对于a,b,有m’=n,n’=m-k\times n使得a\times m’+b\times n’=d成立$
(这里证得了若对于[0,n]满足上式,则[0,n+1]满足了上式)
$故对于任意a,b,d=(a,b),\exists m,n 使得 a\times m+b\times n=d$
那么这个判断方式的原理就很清楚了:
首先是如果$a\times x\equiv 1\pmod m$(这里把逆元写作x),则也就意味着$\exists x,y\in Z$使得$ax-my=1$,而这个方程有整数解的条件就是$gcd(a,m)=1$,至于为什么…这不就是裴蜀定理吗
古典密码
凯撒密码(经典的移位密码)
假设位移量为k(k就是最关键不能够泄露的参数),明文为x,密码为y,明文和密码都是数字[0,26),和26个字母一一对应.于是:
加密:$e_k(x)=y\equiv x+k\pmod {26}$
解密:$d_k(y)=x\equiv y-k\pmod {26}$
这个东西破译极为简单,直接枚举k就行,k再大也没啥用,毕竟取了模就循环了
仿射密码(稍微高级一点点的移位密码)
仿射密码的两个参数:a,b,也是不能够泄露的,明文为x,密码为y,明文和密码仍然是数字[0,26),和26个字母一一对应.于是:
加密:$e_k(x)=y\equiv ax+b\pmod{26}$
解密:$d_k(y)=x\equiv (y-b)\times a^{-1}\pmod{26}$(这里a的负一次方就是指a在26下的逆元)
这个时候需要注意,既然需要逆元,那就必须要找得出来,所以根据之前讲的,需要满足$gcd(26,a)=1$
按照书上的说法,这个时候问题就出来了,因为能够和26互质的26以下的数只有12个…然后b无论怎么取实际上都等价于在26以内取,所以说,所有的可能性只有$26\times 12$种…显然不怎么安全
但是为什么不能够把a搞得大一点呢?难不成a只能小于26?搞不球懂…反正是上古加密方式,管他的呢
C2:序列密码
对称密码分为分组密码和序列密码(好像也有人叫它流密码…不对好像叫流密码的要多一些)
查了一些资料,大概可以这样区分这两种密码:分组密码是把密码分成块块加密,流密码是把密码一股脑加密
随机数的生成
真随机数生成器TRNG
生成不可复制的真的随机的数,基于物理过程生成
伪随机数生成器PRNG
通过一个初始种子,然后递归(或者递推)的得到一串序列,即伪随机数序列,生成方式如下
$$s_0=seed$$
$$s_n=f(s_{n-1})$$
比如,PRNG的一个例子:线性同余生成器(LCG),就像这个样子:
$$s_0=seed$$
$$s_n=as_{n-1}+b\pmod m $$
当然还有一个例子是梅森旋转算法(Mersenne Twister),由日本科学家 Makoto Matsumoto(松本真)和 Takuji Nishimura(西村拓士)在 1997 年开发,似乎是目前最有效的PRNG算法.至于怎么搞的我也不懂,毕竟没学过线代
从安全角度考虑,这显然是不足够的,虽然说这种随机数一般在统计属性上和真的随机数基本一样,但是似乎只需要知道一部分的$s_i$就可以反推出函数,然后反推出种子,然后就可以通过计算预测接下来的数是什么…而且这种东西可能还有周期,就连梅森旋转算法都有…所以这种随机数用于一般的用途就还行,用于对安全性要求高的,就显然不行
加密安全的伪随机数生成器CSPRNG
这算得上是加强版的PRNG,有这样一个性质:就算知道一部分密匙序列,也没办法得到后续位
关于CSPRNG实现的一些思考
百度了一下,是这样的:CSPRNG考虑使用了单向散列函数,再加上从真随机源获取了不断变化的种子,从而做到了这一点.
其一是单项散列函数
单项散列函数其实就是哈希(hash)函数,baidu上是这样讲的:
Hash是作用于一任意长度的消息M,返回一固定长度的散列值h:h=H(m)。其中h的长度为m。Hash函数主要用于封装或者数字签名的过程当中,它必须具有如下几个性质:
1.给定h,根据H(M)=h计算M在计算上是不可行的;
2.给定M,要找到另一消息M’。并满足H(m)=H(m’)在计算上是不可行的。
hash的时候其实可以理解为为消息m创建了一个指纹,如果需要验证m是否被修改了,就可以再次H(m),对比一下两次的hash值
而拿上面的线性同余生成器来讲,那就是在生成了密匙之后再加一个hash函数.但是…有什么用啊?还是有点迷…难道是同余得到seed之后只发送hash种子过后的散列值,然后让对方也生成种子的散列值,然后对比?这样倒是可以避免被倒推.
其二是随机源
据说CPU里面专门搞了一块来生成随机数.通过侦测电脑的各种突发事件的各种参数来获得随机数,比如电压的变化,IO操作的时间变化等等.感觉挺随机的哈.
应该是说,CSPRNG不会太高频率的读取seed,不然效率太低了吧哈哈
序列密码的加密和解密
这里使用模2运算:$x_i$为明文第i位,$y_i$为密文第i位,$s_i$为密匙第i位,明文,密文,密匙,都转化为01字符串,则加密解密方式如下,正确性可自行推导:
$$e_{s_i}(x_i)\equiv x_i+s_i \pmod 2$$
$$d_{s_i}(x_i)\equiv y_i+s_i\pmod 2$$
其实这个东西,和异或XOR是一个样的:相异为1,相同为0.而异或显然是一个非常舒服的加密函数,因为假设密匙的值是随机的话(0,1等概率出现),那么密文中0,1也是等概率的,真好
但是密匙怎么搞呢?一般使用随机数来搞.
无条件安全与一次一密(OTP)
如何定义一个完美的密匙呢?看看无条件安全的定义:
如果一个密码体制在无限计算资源的情况下也不能被破译,则说明它是无条件安全的,也可以叫做信息理论上安全的
那么按照这个过于理想化的定义,如何构建一个无条件安全的密码呢?那就是一次一密(OTP)
一个OTP的密码需要满足如下条件:
1.通过TRNG生成密匙序列s
2.只有合法的通信方才知道密匙序列
3.每个密匙序列位$s_i$只用一次
这个东西为什么是安全的呢?就算被拿到了密文y,但是对于明文x和密匙s来说,这三者之间每一位都有如下的关系:
$$y_i\equiv x_i+s_i\pmod2$$
知道了y,还有s和x两个未知数,根本没法求好吧(s只有合法的双方才知道),因为就算算力是无穷大的,但这个求解空间也是无穷大的
但这种方法显然非常难以实现…第一个还好说,第二个…如果A给B传信息,A有密匙B没有,然后A找一个可靠的方式传给B密匙…为啥不直接传内容算了…第三个也是,难不成传一个G的文件也要一个G的密匙?算了吧…
实际的序列密码的操作方式
实际一点的序列密码,就是用一个短一点密匙发给双方当做种子,然后在密匙产生器里面搞一波产生非常长的密匙,然后在进行传输什么的
利用PRNG构建密码流
比如吧,可以这样弄:
先生成密匙
$$S_0=seed$$
$$S_{i+1}\equiv AS_i+B\pmod m$$
这里的m假设为100位长,$S_i,A,B\in${$0,1,2…m-1$}公开的参数有m,私密的参数有A,B,种子
然后加密是:
$$y_i\equiv x_i+s_i\pmod 2$$
然后…在知道部分明文的前提下这个加密就可以轻易被搞掉…
假设有人知道了明文的前300位,则可以$s_i\equiv y_i+x_i\pmod 2$来得到密匙序列的前300位
然后,复原了部分密匙,再加上密文本来就是已知的,那么显然就可以列出方程组来解出参数A,B的值,从而破解出密匙了
利用CSPRNG构建密码流
之前的方法被破解掉就是因为PRNG可以推导,而PRNG的生成又是公开的.因此使用CSPRNG就可以解决这个问题了,因为CSPRNG生成的密匙是不可以倒推的
当然,为了双方拿到了简短密匙后通过密匙生成器生成的密匙是一样的,这里的CSPRNG必须是伪随机数生成器,否则双方不可能生成一样的密匙
(其实我一直疑惑…既然简短密匙都可以安全的到达双方手中了,为什么不把要传输的东西也传过去算了,何必加密呢…难道是因为要传输的东西太大?)
(哦哦好吧反应过来了…应该是只需要安全的交换一次密匙,之后就一直用这个密匙加密就ok)
基于移位寄存器(LFSR)生成密码流
移位寄存器可以得到长的伪随机序列,书中讲了线性反馈移位寄存器
然鹅我感觉有点看不球懂..应该是缺了点什么知识.先跳过吧
数据加密标准(DES)和替换算法
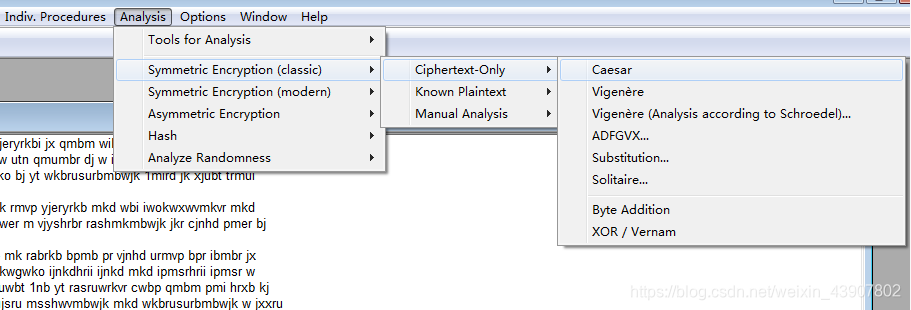
工具使用
CrypTool
词频分析
第一道练习题:移位密码的词频分析和解密中
文本:
Irvmnir bpr sumvbwvr jx bpr lmiwv yjeryrkbi jx qmbm wibpr xjvni mkd ymibrut jx irhx wi bpr riirkvr jx ymbinlmtmipw utn qmumbr dj w ipmhh but bj rhnvwdmbr bpr yjeryrkbi jx bpr qmbm mvvjudwko bj yt wkbrusurbmbwjk 1mird jk xjubt trmui
jx ibndt Wb wi kjb mk rmit bmiq bj rashmwk rmvp yjeryrkb mkd wbi iwokwxwvmkvr mkd ijyr ynib urymwk nkrashmwkrd bj ower m vjyshrbr rashmkmbwjk jkr cjnhd pmer bj lr fnmhwxwrd mkd wkiswurd bj invp mk rabrkb bpmb pr vjnhd urmvp bpr ibmbr jx
rkhwopbrkrd ywkd vmsmlhr jx urvjokwgwko ijnkdhrii ijnkd mkd ipmsrhrii ipmsr w dj kjb drry ytirhx bpr xwkmh mnbpjuwbt 1nb yt rasruwrkvr cwbp qmbm pmi hrxb kj djnlb bpmb bpr xjhhjcwko wi bpr sujsru msshwvmbwjk mkd wkbrusurbmbwjk w jxxru yt bprjuwri wk bpr pjsr bpmb bpr riirkvr jx jqwkmcmk qmumbr cwhh urymwk wkbmvb
分析结果:
基于词频分析的破解
选择第一种模式,根据词频分析
得到结果如下
也可以手动调节,方法就是点下面的Manual analysis
然后…发现原文出锅了…我TM…好家伙…怪说不得怎么都读不懂



