差分约束——1

1.引例

1、一类不等式组的解

给定n个变量和m个不等式，每个不等式形如 x[i] – x[j] <= a[k] (0 <= i, j < n, 0 <= k < m， a[k]已知)，求 x[n-1] – x[0] 的最大值。例如当n = 4，m = 5，不等式组如图一-1-1所示的情况，求x3 – x0的最大值。

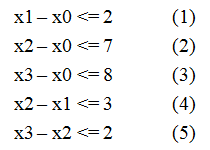
图一-1-1

观察x3 – x0的性质，我们如果可以通过不等式的两两加和得到c个形如 x3 – x0 <= Ti 的不等式，那么 min{ Ti | 0 <= i < c } 就是我们要求的x3 – x0的最大值。于是开始人肉，费尽千辛万苦，终于整理出以下三个不等式：

(3) x3 – x0 <= 8
(2) + (5) x3 – x0 <= 9
(1) + (4) + (5) x3 – x0 <= 7

这里的T等于{8， 9， 7}，所以min{ T } = 7，答案就是7。的确是7吗？我们再仔细看看，发现的确没有其它情况了。那么问题就是这种方法即使做出来了还是带有问号的，不能确定正确与否，如何系统地解决这类问题呢？

让我们来看另一个问题，这个问题描述相对简单，给定四个小岛以及小岛之间的有向距离，问从第0个岛到第3个岛的最短距离。如图一-1-2所示，箭头指向的线段代表两个小岛之间的有向边，蓝色数字代表距离权值。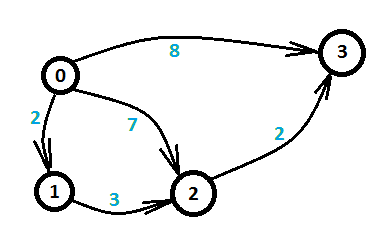

图一-1-2

这个问题就是经典的最短路问题。由于这个图比较简单，我们可以枚举所有的路线，发现总共三条路线，如下：
0 -> 3 长度为8
0 -> 2 -> 3 长度为7+2 = 9
0 -> 1 -> 2 -> 3 长度为2 + 3 + 2 = 7

最短路为三条线路中的长度的最小值即7，所以最短路的长度就是7。

2.差分约束

1、数形结合

如若一个系统由n个变量和m个不等式组成，并且这m个不等式对应的系数矩阵中每一行有且仅有一个1和-1，其它的都为0，这样的系统称为差分约束( difference constraints )系统。引例中的不等式组可以表示成如图三-1-1的系数矩阵。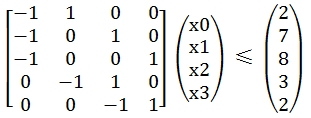

图三-1-1

然后继续回到单个不等式上来，观察

x[i] – x[j] <= a[k]

将这个不等式稍稍变形，将x[j]移到不等式右边，则有

x[i] <= x[j] + a[k]

然后我们令a[k] = w(j, i)，再将不等式中的i和j变量替换掉，i = v， j = u，将x数组的名字改成d（以上都是等价变换，不会改变原有不等式的性质），则原先的不等式变成了以下形式：

d[u] + w(u, v) >= d[v]。

这时候联想到SPFA中的一个松弛操作：

if(d[u] + w(u, v) < d[v]) 
{
    d[v] = d[u] + w(u, v);
}

对比上面的不等式， 两个不等式的不等号_正好相反_

但是再仔细一想，其实它们的逻辑是一致的，因为SPFA的松弛操作是在满足小于的情况下进行松弛，力求达到

d[u] + w(u, v) >= d[v]

而我们之前令a[k] = w(j, i)，所以我们可以将每个不等式转化成图上的有向边：

对于每个不等式 x[i] – x[j] <= a[k]，对结点 j 和 i 建立一条 j -> i的有向边，边权为a[k]，则

！！！敲马桶！！！

求x[n-1] – x[0] 的最大值就是求 0 到n-1的最短路。

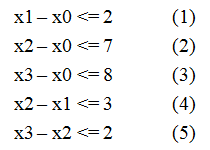
图三-1-1

图三-1-2

图三-1-2 展示了 图三-1-1的不等式组转化后的图。

2、三角不等式

如果还没有完全理解，我们可以先来看一个简单的情况，如下三个不等式：

B – A <= c (1)
C – B <= a (2)
C – A <= b (3)

我们想要知道C – A的最大值，通过(1) + (2)，可以得到 C – A <= a + c，所以这个问题其实就是求min{b, a+c}。将上面的三个不等式按照 三-1 数形结合 中提到的方式建图，如图三-2-1所示。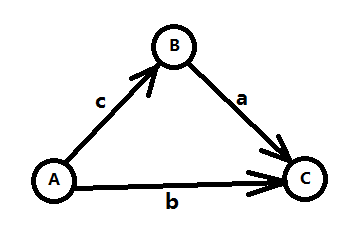

图三-2-1

我们发现min{b, a+c}正好对应了A到C的最短路，而这三个不等式就是著名的 三角不等式 。将三个不等式推广到m个，变量推广到n个，就变成了n个点m条边的最短路问题了。

（min（C-A）=求A到C的最短路）
（min（n-0）=求n到0的最短路）

3、解的存在性

上文提到最短路的时候，会出现负权圈或者根本就不可达的情况，所以在不等式组转化的图上也有可能出现上述情况.

先来看负权圈的情况，如图三-3-1，下图为5个变量5个不等式转化后的图，需要求得是X[t] – X[s]的最大值，可以转化成求s到t的最短路，但是路径中出现负权圈，则表示最短路无限小，即不存在最短路，那么在不等式上的表现即X[t] – X[s] <= T中的T无限小，得出的结论就是 X[t] – X[s]的最大值 不存在。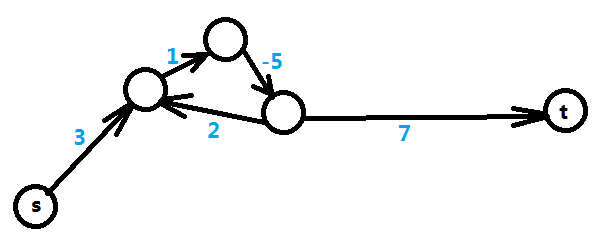

图三-3-1

再来看另一种情况，即从起点s无法到达t的情况，如图三-3-2，表明X[t]和X[s]之间并没有约束关系，这种情况下X[t] – X[s]的最大值是无限大，这就表明了X[t]和X[s]的取值有无限多种。

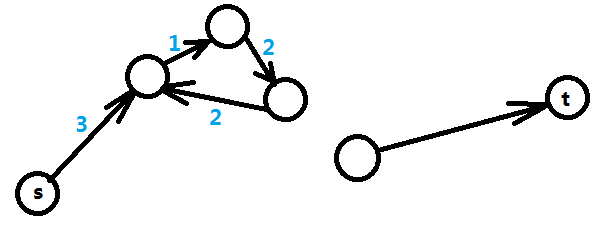
图三-3-2

在实际问题中这两种情况会让你给出不同的输出。

综上所述，差分约束系统的解有三种情况：1、有解；2、无解；3、无限多解；

4、最大值 => 最小值

然后，我们将问题进行一个简单的转化，将原先的”<=”变成”>=”，转化后的不等式如下：

原先：
B – A <= c (1)
C – B <= a (2)
C – A <= b (3)
现在：
B – A >= c (1)
C – B >= a (2)
C – A >= b (3)

然后求C – A的最 小 值（不是最大值！！！最大值最小，最小值最大），类比之前的方法，需要求的其实是max{b, c+a}，于是对应的是下图从A到C的最长路。同样可以推广到n个变量m个不等式的情况。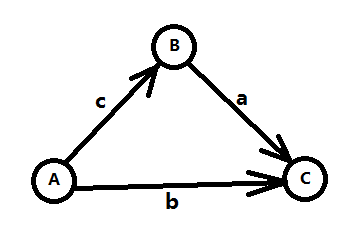

5、不等式标准化

如果给出的不等式有”<=”也有”>=”，又该如何解决呢？

很明显，首先需要关注最后的问题是什么

如果需要求的是两个变量差的最大值，那么需要将所有不等式转变成”<=”的形式，建图后求最短路；相反，如果需要求的是两个变量差的最小值，那么需要将所有不等式转化成”>=”，建图后求最长路。

如果有形如：A – B = c 这样的等式呢？我们可以将它转化成以下两个不等式：

A – B >= c (1)
A – B <= c (2)

再通过上面的方法将其中一种不等号反向，建图即可。
最后，如果这些变量都是整数域上的，那么遇到A – B < c这样的_不带等号_的不等式，我们需要将它转化成”<=”或者”>=”的形式，即 :

A – B <= c – 1

关于求最长路

求最短路的算法太多了，但最长路就要特殊一些，
在一个无负环的图中，若点v到u的路径中有环，则最长路是无解的，即为正无穷，若无环才可以解出v到u的最长路