part Ⅰ

设$x=(x1,x2,…,xn)$是差分约束系统$Ax≤b$的一个解，d为任意常数

则$x+d=(x1+d,x2+d,…,xn+d)$也是该系统$Ax≤b$的一个解

而我们看到的算法解决的问题也就是:在确定一个未知数的情况下,求出这个不等式组中每个$a_i$的符合不等式的最大值(为什么?接着看吧)

部分资料里面讲:由于不等式$x_i<=x_j+k$和最短路里面的松弛条件:

if(dis[v]>dis[f]+edge[i].w)
    dis[v]=dis[f]+edge[i].w;

颇有相像之处,于是我们可以用最短路来解决这个问题,具体操作就是对于$x_i<=x_j+k$这个不等式,需要从$x_j$向$x_i$连一条权值为k的边

~~蒟蒻抠破头皮都没怎么想出来如何理解这个说法~~,于是用了另外一种方法理解:

对于任意的一个点$x_i$,假设有如下约束关系:

$$
x_i<=x_a+k_a, \
x_i<=x_b+k_b,
x_i<=x_c+k_c,
x_i<=x_d+k_d,
x_i<=x_e+k_e
$$

画成图就是这样: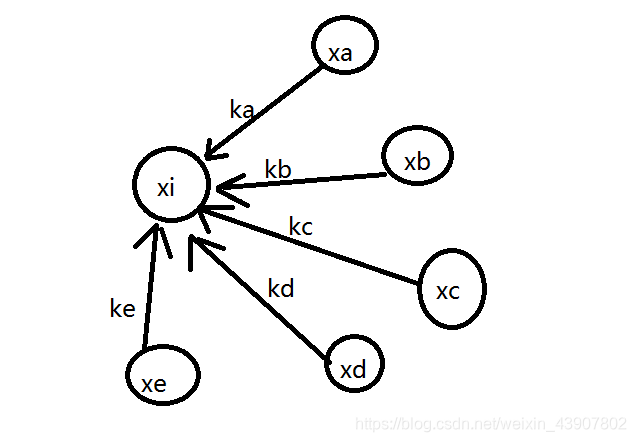
在这里插入图片描述

显然.对于上面的不等式,我们人工来解的时候一定是同小取小,也就是取

$x_j+k_j(j=a,b,c,d,e)$

的最小值

同样的,在最短路算法里面,当你跑完一次最短路的时候

$x_i$一定是$x_j+k_j(j=a,b,c,d,e)$的最小值

并且这个$x_i$就是满足这个约束条件的最大值

关于这个”xi就是满足这个约束条件的最大值”还有另一种理解方式

我们给$x_i<=x_j+k_j$赋予一个意义:$x_i$比$x_j$最多多$k_j$

那么对于任意一个$x_i$,都会有大于等于0个$x_j$来约束它,如果有一个$x_j=5$比$x_i$最多少3,另一个$x_j=2$比$x_i$最多少1,那么这个时候$x_i$能够取到的最大值就只第二个$x_j$的值加上1,也就是3了

也就是说,通过分析$x_i$被$x_j$的约束情况就可以知道这样建图最后求出来的值究竟是最大还是最小了

最后发现,这不就是这些不等式组和最短路相似的地方吗?~~这就很妙了是吧~~

看来还是大佬说的对,蒟蒻只是无法理解罢了…

现在还有一个问题没有解决:如何确定起点

根据引理,如果我们得到了一组为负数的解,那么将这组解同时加上一个数也是这个系统的一组解

那么我们不妨设一个$x_0=0$,然后对每个$x_i$多写一个不等式:$x_i<=x_0$,也就是$x_i<=x_0+0$,这样的话,以$x_0$为起点跑一个单源最短路,就可以得到所有未知数的最大非正数解了,然后如何处置就随意咯

part Ⅱ

如果不等式中的不等号方向倒转，也就是变成了$ai-aj≤k$怎么办？

注意到不等式是可以反号的，于是可以转化为上面的不等式

当然,也可以不转化

用上面讲到的办法,可以判断出,如果用最长路算法,可以求出每个未知数在约束范围内的最小值,同样,如果设一个$x_0$,那么求出来的解就是最小的非负整数解

当然,事情并不是永远那么一帆风顺

那当你遇到这种不等式的时候怎么办?

$$
a-b>=k_1,
b-c<=k_2,
c-d<=k_3,
d=e,
f-e>=k_4,
f-a<=k_5
$$

首先,关于这个等式$d=e$,可以化为$d<=e,e<=d$

然后,虽然我们可以将这个不等式任意变号然后求最长或最短路,但是我们还是需要看问题,如果问题问的是求xxx的最大值,那么就应该去求最短路,反之就是求最长路

但是,不等式组一定有解吗?

显然不是,总的来讲,有下面几种情况:

第一种情况不再讨论

对于第二种情况,在最长路上就是出现了正环,最短路上就是出现了负环(从正负环的定义和性质出发,给松弛操作赋予意义便可以考虑清楚)

第三种情况,如果以x为起点跑程序的话,和x没有约束关系的值的dis不会被更新