重拾图论

最短路算法

Dijkstra+堆优化（优先队列）

模版：

struct node{
    int e;int nxt;int w;
}edge[maxm<<1];
int head[maxn];
inline void addl(int u,int v,int w){
    edge[cnt].e=v;
    edge[cnt].w=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt++;
}
struct point{
    int pos;int dis;
    friend bool operator <(point a,point b){
        return a.dis>b.pos;
    }
};
int dis[maxn];
priority_queue<point>q;
void dij(){
    clean(dis,0x3f);
    dis[s]=0;
    point x;x.dis=0;x.pos=s;
    q.push(x);
    register int v,w;
    while(!q.empty()){
        point u = q.top();
        q.pop();
        for(int i=head[u.pos];i!=-1;i=edge[i].nxt){
            v=edge[i].e;
            w=edge[i].w;
            if(dis[v]>dis[u.pos]+w){
                dis[v]=dis[u.pos]+w;
                point x;x.dis=dis[u.pos]+w;x.pos=v;
                q.push(x);
            }
        }
    }
    printf("%d",dis[t]);
}
int main(){
    freopen("datain.txt","r",stdin);
    read(n),read(m),read(s),read(t);
    register int u,v,w;
    clean(head,-1);
    loop(i,1,m){
        read(u);read(v);read(w);
        addl(u,v,w);addl(v,u,w);
    }
    dij();
    return 0;
}

SPFA+双端队列优化

struct node{
    int e;int nxt;int w;
}edge[(maxm<<1)+(maxn<<2)];
int head[maxn];
int dis[maxn];
deque<int>q;
inline void addl(int u,int v,int w){
    edge[cnt].e=v;
    edge[cnt].w=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt++;
}
void spfa(){
    clean(dis,-0x3f);
    dis[0]=0;
    q.push_front(0);
    while(!q.empty()){
        int u=q.front();
        q.pop_front();
        for(int i=head[u];i!=-1;i=edge[i].nxt){
            int v=edge[i].e;
            if(dis[v]<dis[u]+edge[i].w){//这里是求最长路，最短路的话把不等号方向变一下即可
                dis[v]=dis[u]+edge[i].w;
                if(!q.empty()&&dis[q.front()]<dis[v])
                    q.push_front(v);
                else
                    q.push_back(v);
            }
        }
    }
    printf("%d",dis[s]);
}

差分约束问题

三角不等式:

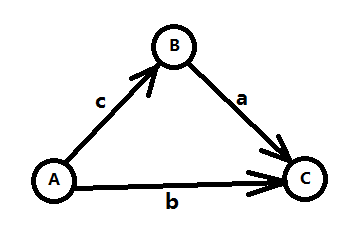
理解问题的关键在利用三角不等式来理解不等式和最短路的关系。从A到C的最短路由从A到B的距离+从B到C的距离之和和从A到C的距离这二者的大小关系决定，x3-x1的最大值由x2-x1的最大值和x3-x2的最大值和x3-x1的已有的最大值约束条件决定。这就是二者的关系。

同时，利用三角不等式可以判断出，最小值就是最长路，最大值就是最短路

可以看一下下面的文章。

国集dalao的论文
自己写的浅析

Floyd

核心思想：两点之间的最短距离为两点之间的当前距离和引入中介节点后的距离之中取最短

loop(v,1,n){
    loop(i,1,n){
        loop(j,1,n){
            f[i][j]=min(f[i][j],f[i][v]+f[v][j])
        }
    }
}

并查集

基本是实现集合合并操作：

int fa[maxn];
int findfa(int u){return fa[u]=(fa[u]==u)?u:findfa(fa[u]);}
inline void merge(int u,int v){fa[findfa(u)]=findfa(v);}
inline bool query(int u,int v){return finfa(u)==findfa(v);}

最小生成树

原理讲解

kruskal

#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(int i=start;i<=end;++i)
#define max(a,b) ((a>b)?a:b)
#define min(a,b) ((a<b)?a:b)
#define ll long long
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define anti_loop(i,start,end) for(int i=start;i>=end;--i)
template<typename T>void read(T &x){
    x=0;char r=getchar();T neg=1;
    while(r>'9'||r<'0'){if(r=='-')neg=-1;r=getchar();}
    while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
    x*=neg;
}
int n,m;
const int maxn = 5000+10;
const int maxm=2e5+10;
struct line{
    int s;int e;ll w;
    friend bool operator <(line a,line b){
        return a.w > b.w;
    }
}edge[maxm];
int fa[maxn];
inline int findfa(int u){return fa[u]=(fa[u]==u?u:findfa(fa[u]));}
inline void merge(int u,int v){fa[findfa(u)]=findfa(v);}
void Kruskal(){
    int nfe=0;ll res=0;
    sort(edge+1,edge+1+m);
    register int u,v;ll w;
    loop(i,1,m){
        u=edge[i].s;
        v=edge[i].e;
        w=edge[i].w;
        if(findfa(u)!=findfa(v)){
            //printf("%d %d\n",u,v);
            merge(u,v);
            ++nfe;
            res += w;
        }
        if(nfe>=n-1){
            printf("%lld",res);
            return;
        }
    }
    printf("orz");
    return;
}
int main(){
    freopen("datain.txt","r",stdin);
    read(n);read(m);
    loop(i,1,n)fa[i]=i;
    loop(i,1,m){
        read(edge[i].s);
        read(edge[i].e);
        read(edge[i].w);
    }
    Kruskal();
    return 0;
}

prim

#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(int i=start;i<=end;++i)
#define max(a,b) ((a>b)?a:b)
#define min(a,b) ((a<b)?a:b)
#define ll long long
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define anti_loop(i,start,end) for(int i=start;i>=end;--i)
#define gc() getchar()
template<typename T>void read(T &x){
    x=0;T neg=1;char r=gc();
    while(r>'9'||r<'0'){if(r=='-')neg=-1;r=gc();}
    while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=gc();}
    x*=neg;
}
int n,m;
const int maxn = 5000+10;
const int maxm = 2e5+10;
struct node{
    int e;int w;int nxt;
}edge[maxm<<1];
struct sort_node{
    int pos;int dis;
    friend bool operator <(sort_node a,sort_node b){
        return a.dis>b.dis;
    }
};
int head[maxn];
int cnt=0;
inline void addl(int u,int v,int w){
    edge[cnt].e=v;
    edge[cnt].w=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt++;
}
priority_queue<sort_node>q;
int dis[maxn];
bool vis[maxn];
void prim(){
    int res=0;
    clean(vis,0);
    clean(dis,0x3f);
    dis[1]=0;
    sort_node x;x.dis=dis[1];x.pos=1;
    q.push(x);
    register int u,v,cnt=0;
    while(!q.empty()){
        sort_node f=q.top();
        cnt++;
        u=f.pos;
        q.pop();
        if(vis[u])continue;
        vis[u]=true;
        res += f.dis;
        for(int i=head[u];i!=-1;i=edge[i].nxt){
            v=edge[i].e;
            if(!vis[v]&&dis[v]>edge[i].w){
                dis[v]=edge[i].w;
                sort_node y;y.dis=dis[v];y.pos=v;
                q.push(y);
            }
        }
    }
    if(cnt>=n)printf("%d",res);
    else printf("orz");
}
int main(){
    freopen("datain.txt","r",stdin);
    read(n);read(m);
    clean(head,-1);
    register int xi,yi,zi;
    loop(i,1,m){
        read(xi);read(yi);read(zi);
        addl(xi,yi,zi);
        addl(yi,xi,zi);
    }
    prim();
    return 0;
}