DP·从入门到递归入门
最最基础的线性DP
数字三角形
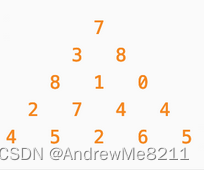
给出下面的数字金字塔,求一条从最高点到底部任意处结束的路径,使得这条路径经过的数字的和最大。每一步可以向左下或者右下走
输入金字塔,输出最大的和
经典DP,当年的IOI赛题
方程:$f[x][y]=max(f[x+1][y],f[x+1][y+1])+a[x][y]$
[NOIP1996 提高组] 挖地雷
题目描述
在一个地图上有N个地窖(N≤20),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入格式:
有若干行。第1行只有一个数字,表示地窖的个数N。第2行有N个数,分别表示每个地窖中的地雷个数。第3行至第N+1行表示地窖之间的连接情况
第3行有n−1个数(0或1),表示第一个地窖至第2个、第3个、…、第n个地窖有否路径连接。
第4行有n−2个数,表示第二个地窖至第3个、第4个、…、第n个地窖有否路径连接。
… …
第n+1行有1个数,表示第n−1个地窖至第n个地窖有否路径连接。(为0表示没有路径,为1表示有路径)。
输出格式:
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
线性DP,方程:$dp[i]$指以i结尾的最长方案数,则
$dp[i]=dp[j]+w[i],j\in {1,2,3,4…n}$
最大食物链
输入格式
第一行,两个正整数 n、m,表示生物种类 n和吃与被吃的关系数 m。
接下来 m 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 80112002的结果。
树形DP:设f[u]为以u结尾的食物链的长度
方程:$f[u]=\sum f[v]$
背包问题
[NOIP2005 普及组] 采药
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
01背包,方程: $f[i][j]=max(f[i-1][j-v[i]]+w[i],f[i-1][j])$
P1616 疯狂的采药
LiYuxiang 是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同种类的草药,采每一种都需要一些时间,每一种也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是 LiYuxiang,你能完成这个任务吗?
此题和原题的不同点:
A:每种草药可以无限制地疯狂采摘。
B:药的种类眼花缭乱,采药时间好长好长啊!师傅等得菊花都谢了!
完全背包,方程:
$f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i],f[i-1][j-2v[i]]+2w[i]..)$
$f[i][j-v[i]]=max(f[i-1][j-v[i]],f[i-1][j-2v[i]]+w[i],f[i-1][j-3v[i]]+2w[i]..)$
故综合上式:
$f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])$
5 倍经验日
现在 absi2011 拿出了 x 个迷你装药物(嗑药打人可耻…),准备开始与那些人打了。
由于迷你装药物每个只能用一次,所以 absi2011 要谨慎的使用这些药。悲剧的是,用药量没达到最少打败该人所需的属性药药量,则打这个人必输。例如他用 2 个药去打别人,别人却表明 3 个药才能打过,那么相当于你输了并且这两个属性药浪费了。
现在有 n 个好友,给定失败时可获得的经验、胜利时可获得的经验,打败他至少需要的药量。
要求求出最大经验 s,输出 5s。
01背包,方程:
$f[i][j]=max(f[i-1][j]+lose[i],f[i-1][j-use[i]]+win[i])\ (j-use[i]>=0)$
$f[i][j]=f[i-1][j]+lose[i]\ (j-use[i]<0)$
LIS和LCS相关
[NOIP1999 普及组] 导弹拦截
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是≤50000的正整数),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
第一问求一个最长不上升子序列,第二问求一个最长上升子序列
以最长不上升子序列为例,设f[i]为以第i个数为结尾的最长不上升子序列长度,则:$f[i]=f[j]+1$,简单递推可得到n方的算法
但是有nlogn的算法:https://www.cnblogs.com/itlqs/p/5743114.html

也可以用数据结构优化也可以达到nlogn的复杂度:
https://blog.csdn.net/weixin_43907802/article/details/96433490
int x,cnt=0;clean(f,0);clean(f1,0x3f);
while(scanf("%d",&x)!=EOF)
a[++cnt] = x;
f[1]=a[1];f1[1]=a[1];
int loc,len=1,loc1,len1=1;
loop(i,2,cnt){
loc = upper_bound(f+1,f+len+1,a[i],greater <int> ()) - f;
loc1 = lower_bound(f1+1,f1+len1+1,a[i]) - f1;
f[loc] = max(f[loc],a[i]);
f1[loc1] = min(f1[loc1],a[i]);
len = max(len,loc);
len1 = max(len1,loc1);
}
printf("%d\n%d",len,len1);要注意upper_bound和lower_bound的区别
这个题其实就涉及一堆问题:最长下降子序列,最长不上升子序列,最长不下降子序列,最长上升子序列。其实都是一样的。
LCS(最长公共子序列)
给出 1,2,…,n1,2,\ldots,n1,2,…,n 的两个排列 P1P_1P1 和 P2P_2P2 ,求它们的最长公共子序列。
LCS,设f[i][j]为A串以第i个结尾,B串以第j个结尾的最长LCS,方程:
$f[i][j]=max(f[i-1][j-1]+1,f[i][j]) \ A[i]=B[j]$
$f[i][j]=max(f[i-1][j],f[i][j-1]) \ A[i]\neq B[j]$
友好城市
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
LIS变式:对北岸(或南岸)的城市从小到大排序,再求南岸(或北岸)的城市位置的最长不下降序列长度即可。
木棍加工
一堆木头棍子共有n根,每根棍子的长度和宽度都是已知的。棍子可以被一台机器一个接一个地加工。机器处理一根棍子之前需要准备时间。准备时间是这样定义的:
第一根棍子的准备时间为1分钟;
如果刚处理完长度为L,宽度为W的棍子,那么如果下一个棍子长度为Li,宽度为Wi,并且满足L>=Li,W>=Wi,这个棍子就不需要准备时间,否则需要1分钟的准备时间;
计算处理完n根棍子所需要的最短准备时间。比如,你有5根棍子,长度和宽度分别为(4, 9),(5, 2),(2, 1),(3, 5),(1, 4),最短准备时间为2(按(4, 9)、(3, 5)、(1, 4)、(5, 2)、(2, 1)的次序进行加工)。
LIS问题的小修改。
先对宽度降序排序,如果宽度一样则按照长度降序排序,于是就有前面的木棍宽度一定大于后面的木棍,而前面的木棍宽度可能小于后面的木棍。
此时的最优解一定是不上升子序列的最少个数。
而根据Dilworth定理,不上升子序列的最少个数就是最长上升子序列的长度
因此就求最长上升子序列的长度就可以了。
[NOIP2004 提高组] 合唱队形
n 位同学站成一排,音乐老师要请其中的 n−k 位同学出列,使得剩下的 k 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 k 位同学从左到右依次编号为 1,2, … ,k,他们的身高分别为 t1,t2, … ,tk,则他们的身高满足t1<⋯<ti>ti+1> … >tk(1≤i≤k)
你的任务是,已知所有 n 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
求两个东西:求从左到右的LIS和从右到左的LIS
然后对每一个位置i,可以求出以i为最高点需要出列的人数。然后就最后取个min就可以了
尼克的任务
尼克每天上班之前都连接上英特网,接收他的上司发来的邮件,这些邮件包含了尼克主管的部门当天要完成的全部任务,每个任务由一个开始时刻与一个持续时间构成。
尼克的一个工作日为 n 分钟,从第 1 分钟开始到第 n 分钟结束。当尼克到达单位后他就开始干活,公司一共有 k 个任务需要完成。如果在同一时刻有多个任务需要完成,尼克可以任选其中的一个来做,而其余的则由他的同事完成,反之如果只有一个任务,则该任务必需由尼克去完成,假如某些任务开始时刻尼克正在工作,则这些任务也由尼克的同事完成。如果某任务于第 p 分钟开始,持续时间为 t 分钟,则该任务将在第 (p+t−1) 分钟结束。
写一个程序计算尼克应该如何选取任务,才能获得最大的空暇时间。
设f[i]为到达第i个时刻的最大空暇时间,则
(本时刻无任务)$f[i]=f[i+1]+1$
(本时刻有任务)$f[i]=max(f[i],f[i+a[sum])$
编辑距离
设 A 和 B 是两个字符串。我们要用最少的字符操作次数,将字符串 A 转换为字符串 B。这里所说的字符操作共有三种:
删除一个字符;
插入一个字符;
将一个字符改为另一个字符。
A,B 均只包含小写字母。
方程:设$f[i][j]$为A串的前i个字符变为B串的前j个字符的最少操作数
增加:$f[i][j]=f[i-1][j]+1$
删除:$f[i][j]=f[i][j-1]+1$
修改:$f[i][j]=f[i-1][j-1]+(A[i]==B[j])?0:1$
综上:
$f[i][j]=min(f[i-1][j]+1,f[i][j-1]+1,f[i-1][j-1]+(A[i]==B[j])?0:1)$
这道题想了挺久。无论使用闫氏DP法还是用之前欧阳讲的“最后一步倒推”,关键都是在于理解最后一步的含义。这里的最后一步,无非就三种情况:
- 如果是增加来的,那么增加之前一定是$f[i][j-1]$,因为A的前i和B的前j-1已经一致了,那么要让A的前i和B的前j一致,则必须要在$f[i][j-1]$中所代表的A串的末尾再加上B[j]这个字符
- 如果是删除来的,那么删除之前一定是$f[i-1][j]$
- 如果是修改来的,那么修改之前一定是$f[i-1][j-1]$
因此以后在思考DP的时候回溯的时候,可以问问自己:回溯之前是什么状态?
luogu P4933 大师
ljt12138 首先建了 个特斯拉电磁塔,这些电塔排成一排,从左到右依次标号为 1 到 n ,第 i 个电塔的高度为 h[i] 。
建筑大师需要从中选出一些电塔,然后这些电塔就会缩到地下去。这时候,如果留在地上的电塔的高度,从左向右构成了一个等差数列,那么这个选择方案就会被认为是美观的。
建筑大师需要求出,一共有多少种美观的选择方案,答案模 998244353。
注意,如果地上只留了一个或者两个电塔,那么这种方案也是美观的。地上没有电塔的方案被认为是不美观的。
同时也要注意,等差数列的公差也可以为负数。
线性DP:设$f[i][j]$为以i为结尾的,公差为j的方案数,则有
$f[i][j]=\sum (f[k][j]+1),(h[k]-h[i]=j)$
因此不难想到一个$O(N^2V)$的算法,就是先找j,再找i,再找k
但是其实可以发现,当i和k确定了后,j就确定了,因此可以直接枚举i和k,就可以转移,复杂度为$O(N^2)$
loop(i,1,n){
res++;
loop(j,1,i-1){
f[i][h[j]-h[i]+v] = (f[i][h[j]-h[i]+v] + f[j][h[j]-h[i]+v] + 1)%mod;//yuan lai de fang cheng xie cuo le
res = (res + f[j][h[j]-h[i]+v] + 1)%mod;
}
}
printf("%lld",res);[NOIP2012 普及组] 摆花
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n 种花,从 1 到 n 标号。为了在门口展出更多种花,规定第 i 种花不能超过 ai 盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
线性DP:设f[i][j]为前i种花放入前j个位置中,则方程为
$f[i][j]=\sum_{k=0}^{min(j,a[i])}f[i-1][j-k]$
但是一个很迷的事情就是,一种花可不可以完全不放。按理来讲是不行的。但是代码里面又不一样了。
loop(i,1,a[1])f[1][i]=1;
loop(i,1,n)f[i][0]=1;
loop(i,2,n){
loop(j,1,m){
loop(k,0,min(j,a[i])){//如果必须要放的话那应该从1开始遍历才对
f[i][j] = (f[i-1][j-k] + f[i][j])%mod;
}
}
}printf("%lld\n",f[n][m]%mod);「一本通 5.1 练习 1」括号配对
Hecy 又接了个新任务:BE 处理。BE 中有一类被称为 GBE。以下是 GBE 的定义:
- 空表达式是 GBE
- 如果表达式 A 是 GBE,则 [A] 与 (A) 都是 GBE
- 如果 A 与 B 都是 GBE,那么 AB 是 GBE
下面给出一个 BE,求至少添加多少字符能使这个 BE 成为 GBE。
线性DP,设f[i][j]为区间[i,j]形成合法括号序列的最少添加字符数,考虑最后一步:
- 可以将区间[i,j]分成两个部分,让两个部分成为GBE,然后把它们拼起来
- 如果区间的左边的字符是[或者(,那么就可以考虑让区间[i+1,j]变成GBE然后在区间右边加一个]或者)
- 如果区间的右边的字符是)或者],那么就可以考虑让区间[i,j-1]变成GBE然后在区间左边加一个(或者[
- 如果区间左右两边恰好是一堆括号,那么就只需要让中间的部分,即[i+1,j-1]为GBE也是可行的
因此方程为:
f[i][j] = min(f[i][j],f[i][k]+f[k+1][j]);
if((s[i-1]=='['&&s[j-1]==']')||(s[i-1]=='('&&s[j-1]==')'))
f[i][j] = min(f[i][j],(len==2?0:f[i+1][j-1]));
else if(s[i-1]=='('||s[i-1]=='[')
f[i][j] = min(f[i+1][j] + 1,f[i][j]);
else if(s[j-1]==']'||s[j-1]==')')
f[i][j] = min(f[i][j-1] + 1,f[i][j]);luogu P5858 「SWTR-03」Golden Sword
小 E 不幸在一场战斗中失去了他的金宝剑。制造一把金宝剑需要 $n$ 种原料,编号为 $1$ 到 $n$,编号为 $i$ 的原料的坚固值为 $a_i$。
炼金是很讲究放入原料的顺序的,因此小 E 必须按照 $1$ 到 $n$ 的顺序依次将这些原料放入炼金锅。
但是,炼金锅的容量非常有限,它最多只能容纳 $w$ 个原料。所幸的是,每放入一个原料之前,小 E 可以从中取出一些原料,数量不能超过 $s$ 个。
我们定义第 $i$ 种原料的耐久度为:放入第 $i$ 种原料时锅内的原料总数(包括正在放入的原料) $\times\ a_i$,则宝剑的耐久度为所有原料的耐久度之和。
小 E 当然想让他的宝剑的耐久度尽可能得大,这样他就可以带着它进行更多的战斗,请求出耐久度的最大值。
注:这里的“放入第 $i$ 种原料时锅内的原料总数包括正在放入锅中的原料,详细信息请见样例。
样例输入 #1
5 3 3
1 3 2 4 5样例输出 #1
40「样例说明」
对于样例 1,一种可行的最优方案为:
首先放进原料 1,此时锅内有 $1$ 种原料,耐久度为 $1\times a_1=1\times 1=1$。
再放进原料 2,此时锅内有 $2$ 种原料,耐久度为 $2\times a_2=2\times 3=6$。
再放进原料 3,此时锅内有 $3$ 种原料,耐久度为 $3\times a_3=3\times 2=6$。
取出原料 1,再放进原料 4,此时锅内有 $3$ 种原料,耐久度为 $3\times a_4=3\times 4=12$。
取出原料 4,再放进原料 5,此时锅内有 $3$ 种原料,耐久度为 $3\times a_5=3\times 5=15$。
最终答案为 $1+6+6+12+15=40$。
线性DP:设f[i][j]为前i个原料放入有j个物品的锅(包括当前这个物品)的最大耐久度,则:
$f[i][j]=max(f[i−1][k]+ai×j)$
其中$j−1≤k≤min(m,j+s−1)$
不过对于这道题,上面的方法有着$O(n^2w)$的复杂度,显然是过不了的。不过不难发现上面方程中max那一堆可以使用单调队列优化,因此复杂度降低一个w,就可以过了
至于单调队列是咋搞的,看这个
区间DP
区间DP的核心就是在各个决策中找到一个连续的区间。只要有这个区间,那么就可以考虑一下区间DP
[NOIP2003 提高组] 加分二叉树
设一个 n 个节点的二叉树 tree 的中序遍历为(1,2,3,…,n)\,其中数字 1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di,tree及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree 的左子树的加分 × subtree 的右子树的加分 + subtree 的根的分数。
若某个子树为空,规定其加分为 1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为 (1,2,3,…,n)且加分最高的二叉树 tree。要求输出:
tree 的最高加分。
tree 的前序遍历。
复习一下前中后序遍历先:

因此本题中,根据前序遍历的特性可设f[l][r]为区间[l,r]构成的子树的最大分数,有方程:
$f[l][r]=max(f[l][k-1]*f[k+1][r]+f[k][k]),f[k][k]=Score[k]$
[NOI1995] 石子合并
在一个圆形操场的四周摆放 $N$ 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。
区间DP:
定义状态f[i][j],表示i到j合并后的最大得分,则有状态转移方程:
$f[i][j] = max(f[i][k] + f[k+1][j] + d(i,j))$
其中,$1<=i<=<=k<j<=N$
[NOIP2006 提高组] 能量项链
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链。在项链上有 $N$ 颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为 $m$,尾标记为 $r$,后一颗能量珠的头标记为 $r$,尾标记为 $n$,则聚合后释放的能量为 $m \times r \times n$(Mars 单位),新产生的珠子的头标记为 $m$,尾标记为 $n$。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 $N=4$,$4$ 颗珠子的头标记与尾标记依次为 $(2,3)(3,5)(5,10)(10,2)$。我们用记号 $\oplus$ 表示两颗珠子的聚合操作,$(j \oplus k)$ 表示第 $j,k$ 两颗珠子聚合后所释放的能量。则第 $4$ 、 $1$ 两颗珠子聚合后释放的能量为:
$(4 \oplus 1)=10 \times 2 \times 3=60$。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为:
$((4 \oplus 1) \oplus 2) \oplus 3)=10 \times 2 \times 3+10 \times 3 \times 5+10 \times 5 \times 10=710$。
定义状态f[l][r]表示以a[l]开头a[r]结尾的数串的最大和,则有状态转移方程:
$f[l][r]=max(f[l][r],f[l][k]+f[k][r]+a[l]*a[k]*a[r])$,k为i,j之间任一节点
luoguP1220 关路灯
某一村庄在一条路线上安装了 $n$ 盏路灯,每盏灯的功率有大有小(即同一段时间内消耗的电量有多有少)。老张就住在这条路中间某一路灯旁,他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。
为了给村里节省电费,老张记录下了每盏路灯的位置和功率,他每次关灯时也都是尽快地去关,但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯,然后可以向左也可以向右去关灯。开始他以为先算一下左边路灯的总功率再算一下右边路灯的总功率,然后选择先关掉功率大的一边,再回过头来关掉另一边的路灯,而事实并非如此,因为在关的过程中适当地调头有可能会更省一些。
现在已知老张走的速度为 $1m/s$,每个路灯的位置(是一个整数,即距路线起点的距离,单位:$m$)、功率($W$),老张关灯所用的时间很短而可以忽略不计。
请你为老张编一程序来安排关灯的顺序,使从老张开始关灯时刻算起所有灯消耗电最少(灯关掉后便不再消耗电了)。
区间DP:
设f[i][j][0]为关闭区间[i,j]的路灯且最后一个关掉的路灯为区间的左端点的最小功率,f[i][j][1]为关闭区间[i,j]的路灯且最后一个关掉的路灯为区间的右端点的最小功率,则有方程:
$f[i][j][0]=min(f[i+1][j][0]+(pos[i+1]-pos[i])*exsum(i+1,j),f[i+1][j][1]+(pos[j]-pos[i])*exsum(i+1,j))$
$f[i][j][1]=min(f[i][j-1][0]+(pos[j]-pos[i])*exsum(i,j-1),f[i][j-1][1]+(pos[j]-pos[j-1])*exsum(i,j-1))$
其中$exsum(i,j)$为区间$[1,i-1]$和$[j+1,n]$的电灯的功率和,$pos[i]$为第i个电灯的位置
[NOIP2007 提高组] 矩阵取数游戏
帅帅经常跟同学玩一个矩阵取数游戏:对于一个给定的 $n \times m$ 的矩阵,矩阵中的每个元素 $a_{i,j}$ 均为非负整数。游戏规则如下:
- 每次取数时须从每行各取走一个元素,共 $n$ 个。经过 $m$ 次后取完矩阵内所有元素;
- 每次取走的各个元素只能是该元素所在行的行首或行尾;
- 每次取数都有一个得分值,为每行取数的得分之和,每行取数的得分 = 被取走的元素值 $\times 2^i$,其中 $i$ 表示第 $i$ 次取数(从 $1$ 开始编号);
- 游戏结束总得分为 $m$ 次取数得分之和。
帅帅想请你帮忙写一个程序,对于任意矩阵,可以求出取数后的最大得分。
区间DP:设f[i][j]为选的只剩下区间[i,j]的最大和,则有方程:
$f[i][j]=max(f[i-1][j] + a[i-1]*2^{m-(j-i+1)},f[i][j+1] + a[j+1]*2^{m-(j-i+1)})$
不过这个题由于答案会爆long long,因此要么使用__int128要么就写高精度。(而我这么懒,怎么可能写高精度呢)
[USACO16OPEN]248 G
给定一个1*n的地图,在里面玩2048,每次可以合并相邻两个(数值范围1-40),问序列中出现的最大数字的值最大是多少。注意合并后的数值并非加倍而是+1,例如2与2合并后的数值为3。
样例:n=4,地图为1 1 1 2,则:
1 [1 1] 2–> 1 [2 2]–> 1 3,答案为3
题目不难,但是踩了几个坑。区间DP:设f[i][j]为 完全合并区间[i,j] 后该区间得到的最大值,则有
$f[i][j]=max(f[i][k]+1,f[i][j]),(f[i][k]=f[k+1][j])$
一开始头铁写的这个方程:$f[i][j]=max(f[i][j],f[i+1][j],f[i][j-1])(f[i+1][j]=a[i],f[i][j-1]=a[j])$,后面发现问题,错在:区间[i,j]不仅仅可以从比它小一个数的区间更新过来,而是可以从它的任意两个子区间更新过来。可能是被样例误导了。
然后实现的时候,直接loop(i,1,n)loop(j,i+1,n),然后全部WA掉。错在枚举顺序:这个方程中要从小区间更新大区间,而不是只需要枚举完每一个区间就行。
[CQOI2007]涂色
假设你有一条长度为 5 的木板,初始时没有涂过任何颜色。你希望把它的 5 个单位长度分别涂上红、绿、蓝、绿、红色,用一个长度为 5 的字符串表示这个目标:RGBGR。
每次你可以把一段连续的木板涂成一个给定的颜色,后涂的颜色覆盖先涂的颜色。例如第一次把木板涂成 RRRRR,第二次涂成 RGGGR,第三次涂成 RGBGR,达到目标。用尽量少的涂色次数达到目标。
区间DP:设f[i][j]为区间[i,j]涂完需要的最少次数,则有方程
$f[i][j]=min(f[i+1][j],f[i][j-1]),s[i]==s[j]$
$f[i][j]=min(f[i][k]+f[k+1][j]),s[i]\neq s[j]$
这题自己没想出来,看题解做出来的。状态表示猜都猜得到,必然是f[i][j],但是转移的时候完全不知道怎么转移。主要是没有理解到:
- 区间[i,j]端点颜色相同,则意味着从[i+1,j]或者[i,j-1]涂色涂到[i,j]根本不需要额外的花费,可以直接一笔画完整个区间
- 如果区间[i,j]端点颜色不相同,则说明区间[i,j]不能够从[i+1,j]或者[i,j-1]这两个子区间没有额外花费的转移来,因此只能分成f[i][k]和f[k+1][j]两个子区间来转移,且这两个子区间的涂色次数是通过相加的方式来合并的(可以搞组数据手模一下)