• 可分离变量的一阶微分方程
    • 分离变量求微分方程
  • 齐次一阶微分方程$\frac{dy}{dx}=f(\frac{y}{x})\ \ or \ \frac{dy}{dx}=f(\frac{x}{y})$
    • 如果满足齐次，则使用换元法$u=\frac{y}{x}$或者$u=\frac{x}{y}$将该类型微分方程化为可分离变量的方程
    • 如果出来的是：$\frac{dy}{dx}=f(\frac{ax+by+c}{a_1x+b_1y+c_1}),c\times c_1\neq 0$，则使用换元法（$x=X+h,y=Y+k$）将c和c1消掉，利用系数行列式$\left|
      \begin{array}{cccc}
      a & b\
      a_1 & b_1\
      \end{array}
      \right|$是否等于0来判断是否能不能通过换元消去c和c1。
      • 如果可以，则可以化为齐次一阶微分方程，从而求解，再换元回来即可。
      • 如果不可以，则可以用换元法$\lambda=\frac{a_1}{a}=\frac{b_1}{b},v=ax+by$将方程化为可分离变量的方程
  • 一阶线性微分方程$\frac{dy}{dx}+P(x)y=Q(x)$
    • 当右侧函数为0时，则为一阶齐次线性方程，则可分离变量得到方程的通解为$y=Ce^{-\int P(x)dx}$
    • 当右侧函数不为0时，则为一阶非齐次线性方程，则可通过常数变易法（也可通过指数求导特征来理解）得到通解$y=e^{-\int P(x)dx}(\int Q(x)e^{\int P(x)dx}+C)$
  • 伯努利方程$\frac{dy}{dx}+P(x)y=Q(x)y^n$
    • 同时除以$y^n$，令$z=y^{1-n}$，则可得到一阶线性微分方程$\frac{dz}{dx}+(1-n)P(x)z=(1-n)Q(x)$,代入公式求解即可
  • 二阶线性微分方程
    • 二阶齐次线性微分方程：$\frac{d^2y}{dx^2}+P(x)\frac{dy}{dx}+Q(x)y=0$
      • 其通解为：$y=\sum_{i=1}^n C_iy_i(x),n=2–>y=C_1y_1(x)+C_2y_2(x)$,其中C1,C2为任意常数，y1,y2为方程的两个特解，y1、y2线性无关
    • 二阶非齐次线性微分方程：$\frac{d^2y}{dx^2}+P(x)\frac{dy}{dx}+Q(x)y=f(x)$
      • 其通解为：$y=C_1y_1+C_2y_2-y_1\int\frac{y_2f}{W}dx+y_2\int\frac{y_1f}{W}dx$
      • 其中，$y_1,y_2$是对应的齐次线性方程的特解，$W=\left|
        \begin{array}{cccc}
        y_1 & y_2\
        y_1^{‘} & y_2^{‘}\
        \end{array}
        \right|\neq 0$


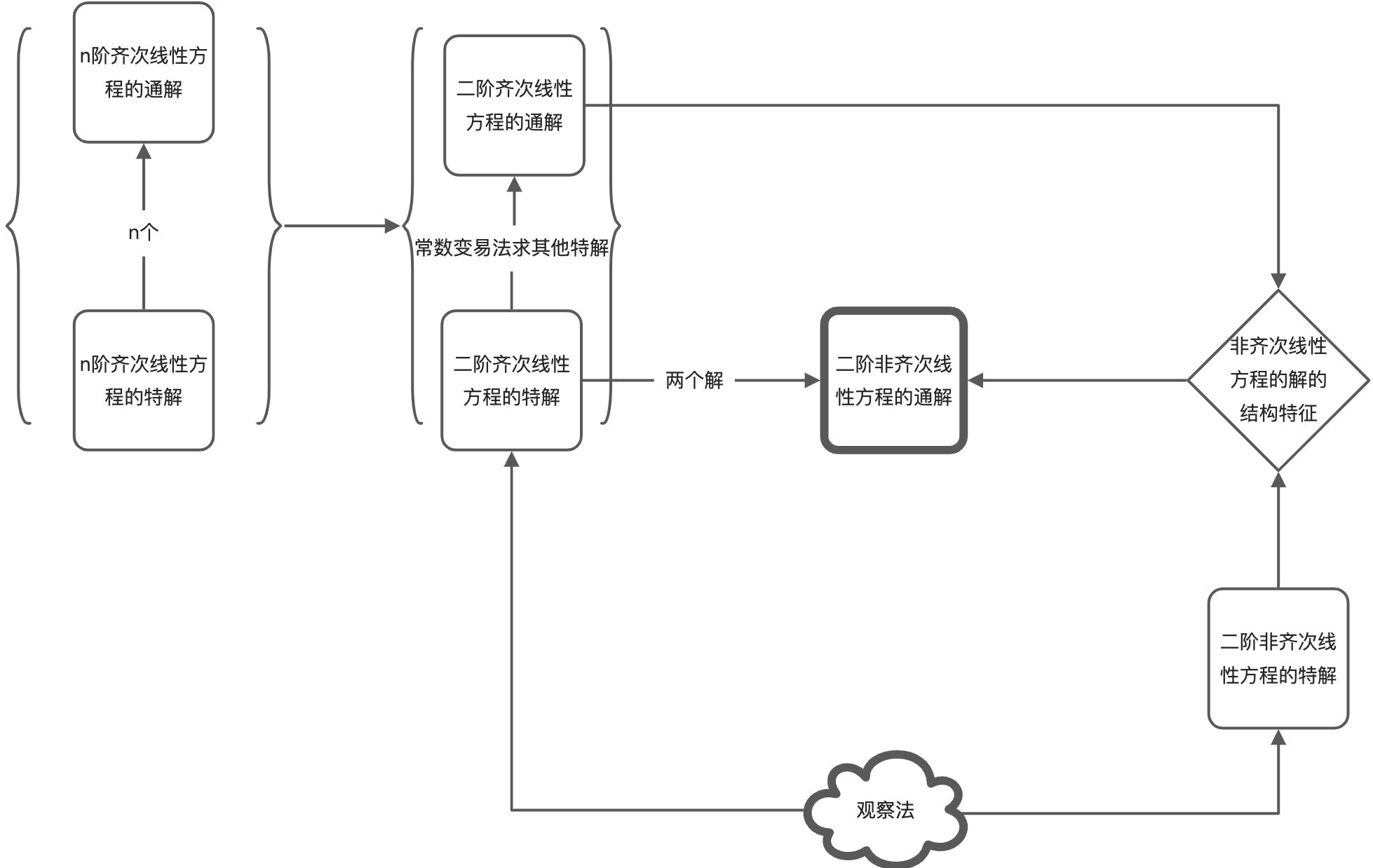
  • 二阶常系数齐次线性微分方程的通解

    • $y^{‘’}+P(x)y^{‘}+Q(x)y=0–>y^{‘’}+py^{‘}+qy=0$
    • 写特征方程：
      • $r^2+pr+q=0$
    • 解出两个根$r=\frac{-p\pm\sqrt{p^2-4q}}{2}$
    • 则
      • r1,r2是两个不相等的实根：$y=C_1e^{r_1x}+C_2e^{r_2x}$
      • r1,r2两个不相等的实根：$y=(C1+C2x)e^{r_1x}$
      • r1,r2是一对共轭负根（$r=\alpha\pm\beta i$）：$y=e^{\alpha}x(C_1\cos\beta x+C_2\sin\beta x)$

  • 二阶常系数非齐次线性微分方程$y^{‘’}+py^{‘}+qy=f(x)$的通解

    • 解题思路：常系数齐次线性微分方程的通解+非齐次特征方程的特解
    • 非齐次特征方程的特解，根据右侧函数的不同形式有不同的解法（只需要掌握这两种即可）
      • 方程形如：$f(x)=e^{\lambda x}P_m(x),P_m(x)=a_0x^m+a_1x^{m-1}+…+a_{m-1}x+a_m$
        • 则特解为：$y=x^kR_m(x)e^{\lambda x}$
      • 方程形如：$f(x)=e^{\lambda x}[P_l(x)\cos\omega x+Q_n(x)\sin\omega x]\O(P_l(x))=x^l,O(Q_n(x))=x^n,P_l(x)\times Q_n(x)\neq0$
        • 应用欧拉公式，则特解为：$y=x^ke^{\lambda x}[R_m^{(1)}(x)\cos\omega x+R_m^{(2)}\sin\omega x]\m=max(l,n)$（P351）

  • 可降阶的高阶微分方程

    • $y^{(n)}=f(x)$，直接积分降阶即可
    • $y^{‘’}=f(x,y^{‘}),y^{‘’}=f(y,y^{‘})$型，这其中y和x无关，换元，令$y^{‘}=p$，则$y^{‘’}=p^{‘},p^{‘}=f(x,p)$,则得到一阶微分方程，可解。
    • $y^{‘’}=f(y,y^{‘})$型，这其中y是x的函数，换元，令$y^{‘}=p$，则$y^{‘’}=\frac{dp}{dx}=\frac{dp}{dy}\frac{dy}{dx}=p\frac{dp}{dy},p\frac{dp}{dy}=f(y,p)$,则得到一阶微分方程，可解。

  • 欧拉方程

    • 是一种特殊的变系数线性微分方程
    • 形式：$x^ny^{(n)}+p_1x^{n-1}y^{(n-1)}+…+p_{n-1}xy^{‘}+p_ny=f(x)$
    • 解法
      • 换元：$x=e^t$，则$D=\frac{d}{dt}–>x^ky^{(k)}=D(D-1)(D-2)…(D-k+1)y$
      • 代入原式，得以t为自变量的常系数线性方程。求解完毕后换元回来即可。